Проектирование установки для гидроиспытаний, страница 15

Отмеченная величина энергии отвечает тому максимальному     количеству  энергии ,  что  может   получить  стенка  в  процессе   установления

 

течения, т.е. в 1-й стадии.

Однако фактическая передача энергии зависит  от отношения 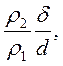 (процесс столкновения главной части струи со стенкой в какой-то степени аналогичный не упругому столкновению куль).

Из закона сохранения легко получаем выражение:

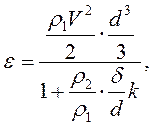 (7.7)

где: ε - энергия передана защитному листу;

к - отношение площади листа, что воспринимает импульс, к площади пересечения струи.

Если   запишем   теперь,   что ε не должно превосходить энергию допустимой деформации листа в области вмятины,  площадь которой    пометим пока через к, 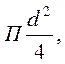  то получим условие не прибивки в 1-й стадии:

<

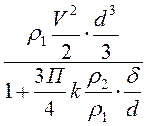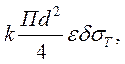
Решаем это неравенство относительно, предварительно заменяя 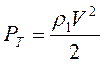 и думая 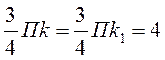, что отвечает значениям k и k1 , близким к реальным , тогда будем иметь:

δ>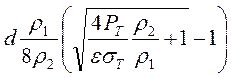  (7.8)

Формулы (7.6) и (7.8) дают одинаковые значения ε при:

 

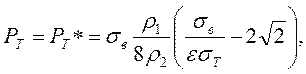 (7.9)

при Р_Т > Р_Т*    большие значения ε дает формула (7.6),  при Р_Т < Р_Т*    -           формула (7.8). Поэтому в зависимости от величины Р_Т нужно применять ту или другую формулу. Если в качество препятствия используется лист из стали 3, то Р_Т*= 20 МПа.

7.3.3. Приближенный расчет вытекания струи

Потому что предварительно неизвестно, какую форму и размеры будет иметь отверстие в стенке посудины в случае его разрыва, при расчете защиты, по-видимому, нужно ориентироваться на худший случай, когда образуется отверстие, что дает струю максимальной пробивной силы.

Точное решение задания о вытекании представляет значительные трудности, однако здесь можно сделать оценки, вполне достаточные для расчета защиты.

Пусть мы имеет посудину объемом V с жидкостью под давлением Р₁.

Избыточный объем жидкости, что из него нужно выпустить, чтоб давление упало к атмосферному, пометим через Δ V1 .

Пусть при t = О в стенке посудины образовалось отверстие с площадью S и характерным размером, (например диаметром) - d.

Волна разжижения, что идет от свободной поверхности внутрь   посудины, снимает давлению вблизи поверхности внутри посудины,       снимает  давление   вблизи   поверхности   к   атмосферному   и   сообщает   поверхностному слою жидкости скорость 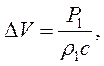 где с – скорость звука в жидкости.

         

Хотя мы здесь имеем дело с пространственным  течением жидкости однако характерное время ускорения жидкости t*  можно оценить за одномерной схемой: волна разжижения в результате резкого расширения поверхности фронта при входе внутрь посудины на расстоянии порядка d от отверстия отбивается назад в виде волны сжатия той же амплитуды (так же, как при прохождении волны разжижения в трубе через область резкого увеличения пересечения).

При этом в пересечении отверстия скорость жидкости увеличивается на ту же величину ΔV. Волна сжатия опять отбивается от свободной поверхности волной разжижения, что увеличивает скорость еще на ΔV  и т.д.

Потому что скорость жидкости в пересечении отверстия увеличивается на величину 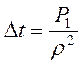 , за время  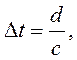то среднее наращивание скорости струи за единицу времени в начале вытекания составит:

.

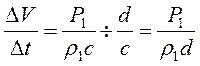Характерным временем процесса разгон струи будет

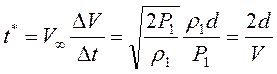, где 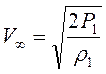 (7.10)

Чтоб учесть влияние изменения давления в посудине в процессе вытекания, применим другой подход: рассчитывать вытекание будем как для несжимаемой жидкости (это оправдано, пока <<1), а сжимает учтем лишь через связь между давлением в посудине и количеством вытекшей жидкости.

Вдоль оси отверстия скорость жидкости V зависит от одной координаты х и t.

Запишем уравнение движения вдоль этой оси:

,

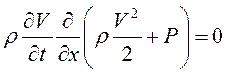Обинтегрируем его по x, думая

;

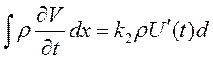где: U'(t) - скорость в пересечении отверстия, числовой коэффициент к₂ =1 поскольку с удалением от отверстия внутрь жидкости скорость убывает достаточно быстро:

приблизительно ~ .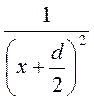

В дальнейшем будем везде уважать, что К = 1. Хотя в целом говоря, немного меняется впоследствии.

После интеграции получим:

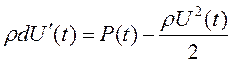, (7.11)