Тяговые расчеты при проектировании железных дорог: Учебное пособие, страница 9

В связи с введением высокоскоростного движения пассажирских поездов и тяжеловесных грузовых поездов, к тормозным системам поезда стали предъявлять повышенные требования. Разрабатываются и внедряются дисковые, электромагнитные и другие принципиально новые системы. Также может применяться комплекс разных тормозных систем, используемых либо совместно, либо раздельно в определенном диапазоне скоростей.

4.4  Тормозные силы при рекуперации

При работе двигателя в генераторном режиме в сеть отдается ток  напряжением . Механическая работа вращения ведущих осей, превращается в электрическую. На валу двигателя образуется тормозной момент. В результате возникает сила рекуперативного или реостатного торможения (рис. 4.2 ).

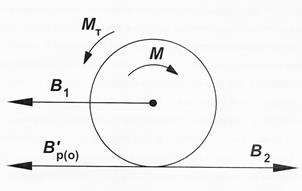
Рис. 4.2 Схема реализации тормозной силы при рекуперации

Электрическая мощность, отдаваемая тяговым электродвигателям в сеть через механическую мощность, определяется по формуле:

,				(4.18)
где		‑	тормозная сила одной оси, кгс.

Из баланса напряжений:

,

(4.19)

или приближенно:

.

(4.20)

Тогда

,				(4.21)
где		‑	КПД при рекуперации (учитывает отсутствие слагаемого ()).

Общая тормозная сила рекуперации определяется по формуле:

.

(4.22)

Произведение () увеличивается с возрастанием скорости, поэтому электрическое торможение обладает свойствами устойчивости: больше скорость ‑ больше сила торможения и наоборот. Этот фактор используется машинистом, если поезд должен двигаться по определенному спуску с установленной скоростью.

Потребная тормозная сила, , может быть определена по формуле:

.

(4.23)

5  Уравнение движения поезда

Кинетическая энергия, Т, Дж, поезда массы , т, (при условии, что колеса катятся без скольжения) определяется по формуле:

,					(5.1)
где		‑		скорость движения поезда;
		‑		момент инерции колесной пары относительно оси вращения;
		‑		угловая скорость вращающихся частей, определяемая по формуле:
,					(5.2)
где			‑	диаметр колеса.

Момент инерции колесной пары относительно оси вращения определяется по формуле:

,				(5.3)
где		‑	масса вращающихся частей;
		‑	радиус инерции вращающихся частей.

Тогда

.

(5.4)

Обозначим суммарную массу вращающихся частей через  и выполним подстановку, тогда выражение (5.1) примет вид:

,

(5.5)

Введем обозначение:

.

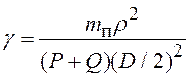Тогда с учетом этого обозначения:

.

(5.6)

Выражение  называется коэффициентом инерции вращающихся масс поезда.

Изменение кинетической энергии поезда на некотором его перемещении составит:

.

(5.7)

Так как в расчетах учитываются только внешние силы, работа внутренних сил поезда равна нулю и ее можно не учитывать. Тогда, согласно закону сохранения энергии, изменение кинетической энергии равно работе сил на пройденном пути:

,				(5.8)
где		‑	касательная (на ободе колеса) сила тяги локомотива;
		‑	общее сопротивление движению поезда;
		‑	тормозная сила;
		‑	путь, пройденный поездом.