передмова
В частині 1 методичних вказівок до практичних занять з навчальної дисципліни „Теорія автоматичного керування” наведені типові задачі і надані рекомендації до їх розв’язання з таких розділів(модулів):
· Принципи автоматичного керування та математичні моделі лінійних неперервних систем автоматичного керування (модуль 1);
· Стійкість лінійних неперервних систем автоматичного керування (модуль 2);
· Якість лінійних неперервних систем автоматичного керування (модуль 3);
В даній частині 2 методичних вказівок до практичних занять приділяється увага розв’язанню задач з інших розділів теорії автоматичного керування, а саме:
· Підвищення якості і синтез лінійних неперервних систем автоматичного керування (модуль 4);
· Математичні моделі, стійкість, якість та корекція дискретних систем автоматичного керування (модуль 5);
· Математичні моделі, стійкість, якість та корекція нелінійних систем автоматичного керування (модуль 6);
· Методи синтезу оптимальних систем автоматичного керування (модуль 7);
· Адаптивні системи автоматичного керування (модуль 8)
· . Типові задачі та рекомендації до їх розв’язання мають
бути використані студентами при підготовці до практичних занять.
1. підвищення якості і синтез лінійних неперервних систем автоматичного керування (модуль 4)
Методичні вказівки
Корекція САК проводиться з метою підвищення якості процесу керування. Якість керування зв’язана з одним із найважливіших показників якості системи – точністю (похибкою) її роботи в усталеному та перехідному режимах.
В поняття точності усталеного режиму входить статична та динамічна точності, а в поняття точності системи в перехідному режимі – величина відхилів керованої координати від заданого значення та тривалість цих відхилів.
Майте на увазі також те, що при корекції САК потрібно одночасно задовольняти двом кардинальним суперечностям в теорії автоматичного керування:
· Суперечності між підвищенням точності в усталеному режимі і запасами стійкості в перехідному режимі;
· Суперечності між підвищенням якості процесу керування і складністю технічної реалізації корегуючих пристроїв.
В тій чи іншій мірі задовольнити вище названим суперечностям можливо тільки за умови правильного вибору потрібного шляху корекції системи.
До основних шляхів підвищення якості керування відносять:
1) Використання замкнутих САК і збільшення коефіцієнта підсилення регулятора (системи);
2) Формування потрібних законів регулювання (введення астатизму, регулювання по похідних);
3) Використання спеціальних структур САК, які реалізують принципи керування, що забезпечують підвищення точності (комбіноване керування, системи із змінною структурою, системи, що допускають необмежене підвищення коефіцієнта підсилення регулятора);
4) Реалізація принципів інваріантності;
5) Використання різного виду корегуючих пристроїв.
Після вибору потрібного шляху корекції системи переходять до синтезу корегуючих ланок.
Параметри корегуючих ланок можуть бути отримані за допомогою різних методів, наприклад, кореневих, інтегральних оцінок, але найчастіше вони розраховуються за допомогою логарифмічних амплітудно-частотних характеристик (ЛАЧХ) з використанням графіків.
В останні часи для синтезу регуляторів в системах автоматичного керування електроприводом часто використовують метод стандартних перехідних функцій. Прикладом таких систем є системи підпорядкованого регулювання координат, регулятори яких забезпечують модульний або симетричний оптимуми.
Для вирішення задач цього розділу рекомендується використати матеріал: [1]– С.228– 286; [2]– С.234– 263; [4]– С.188– 234; [5]– С.185– 205; [9]– С.247– 281; [11]– С.130–194.
1.1 Практичне заняття 1. Корекція САК
1.1.1 Передаточна функція розімкненої системи з астатизмом першого порядку
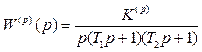 .
(1.1)
.
(1.1)
Визначити
наближеним частотним методом коефіцієнт підсилення ![]() , щоб показник коливальності
М замкненої системи мав значення 1,35. Для цього випадку розрахувати також
коефіцієнт демпфування ξ, приблизні значення перерегулювання σ, часу перехідного
процесу tР, запасу стійкості по фазі Δφ і
частоти зрізу ωЗР, якщо Т1=0,2с, Т2 =0,05с.
, щоб показник коливальності
М замкненої системи мав значення 1,35. Для цього випадку розрахувати також
коефіцієнт демпфування ξ, приблизні значення перерегулювання σ, часу перехідного
процесу tР, запасу стійкості по фазі Δφ і
частоти зрізу ωЗР, якщо Т1=0,2с, Т2 =0,05с.
Розв’язання. У відповідності з [2]– с.206– 213 визначаємо параметри спрощеної моделі
![]() (1.2)
(1.2)
а також коефіцієнт демпфування моделі
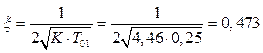 , (1.3)
, (1.3)
де коефіцієнт підсилення моделі вираховується з виразу
![]() (1.4)
(1.4)
Тоді, ураховуючи (1.4), маємо
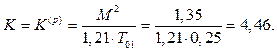 (1.5)
(1.5)
Оскільки коефіцієнт демпфування моделі знаходиться в межах 0,25≤ξ≤ 0,55, то для ξ=0,473 справедливі наближені формули для визначення за умовами задачі показників якості системи, а саме:
![]() (1.6)
(1.6)
![]() (1.7)
(1.7)
![]() (1.8)
(1.8)
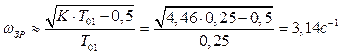 . (1.9)
. (1.9)
1.1.2 Передаточна функція розімкненої системи з астатизмом першого порядку
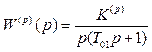 . (1.10)
. (1.10)
Визначити оптимальне співвідношення між параметрами К(Р) і Т розімкненої системи при яких інтегральна квадратична оцінка
![]() (1.11)
(1.11)
де ΔХn– перехідна складова сигналу похибки.
Розв’язання. Передаточна функція замкненої системи по каналу Х0-Х
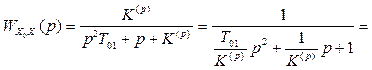
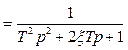 , (1.12)
, (1.12)
де 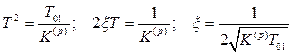 .
.
Передаточна функція системи по каналу Х0-ΔХ
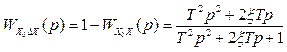 . (1.13)
. (1.13)
Зображення перехідної складової сигналу похибки при одиничному ступінчастому задавальному діянні Х0(t)=1(t) має вигляд
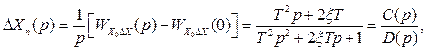 (1.14)
(1.14)
де відповідно [2]–– с.217 n=2; ![]() .
.
Для обчислення квадратичної оцінки по зображенню (1.14) використаємо рівняння Парсеваля
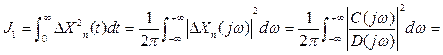
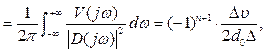 (1.15)
(1.15)
де 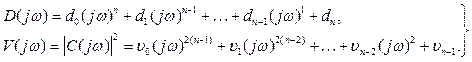 (1.16)
(1.16)
Для обчислювання інтегралу (1.15) запишемо зображення ΔХn(р) у вигляді
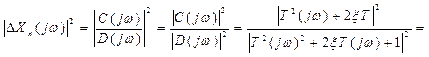
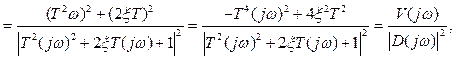 (1.17)
(1.17)
де, у відповідності з (1.16), маємо
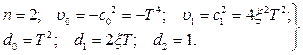 . (1.18)
. (1.18)
Тоді визначники, що входять в [1.15], матимуть значення:
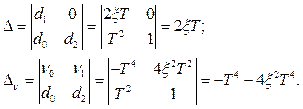 (1.19)
(1.19)
Згідно з [1.15]
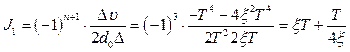 . (1.20)
. (1.20)
Оптимальне
значення коефіцієнта демпфування ![]() визначаємо із виразу
визначаємо із виразу
![]() , (1.21)
, (1.21)
звідки![]() . (1.22)
. (1.22)
Тоді, ураховуючи (1.22), знаходимо оптимальне співвідношення між параметрами K(p) і Т із рівняння
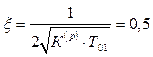 . (1.23)
. (1.23)
Згідно з (1.23)
![]() . (1.24)
. (1.24)
Чи
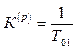 . (1.25)
. (1.25)
1.1.3 Розімкнена слідкуюча система, яка має в собі функціонально необхідні елементи, описується передаточною функцією
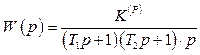 , (1.26)
, (1.26)
де ![]() =0,01с;
=0,01с; ![]() =0,03с;
=0,03с; ![]() =
=![]() .
.
Треба визначити
значення ![]() за умови забезпечення мінімуму
квадратичної інтегральної оцінки для похибки у разі подачі одиничного вхідного
сигналу.
за умови забезпечення мінімуму
квадратичної інтегральної оцінки для похибки у разі подачі одиничного вхідного
сигналу.
Розв’язання. Зображення перехідної складової сигналу похибки у разі подачі одиничного вхідного сигналу
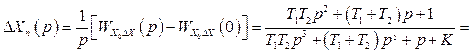
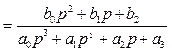 ,
(1.27)
,
(1.27)
де ![]()
![]()
![]() ;
; ![]()
![]() ;
; ![]() ;
; ![]() , n=3.
, n=3.
Для обчислення інтегралу J1 використаємо [1]– с.214, таблиці 5.2, згідно з якою для n=3
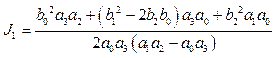 . (1.28)
. (1.28)
На основі таблиці 5.2 по виразу (1.28) обчислимо
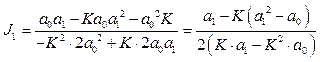 . (1.29)
. (1.29)
Далі знайдемо частинну похідну ![]() і прирівняємо її до нуля:
і прирівняємо її до нуля:
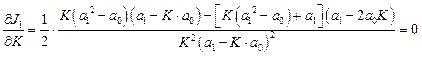 (1.30)
(1.30)
або
![]() . (1.31)
. (1.31)
Підставивши числові значення коефіцієнтів, дістанемо квадратне рівняння
![]() , (1.32)
, (1.32)
звідки оптимальне значення коефіцієнта КОПТ=К(Р)=37.
1.1.4 Передаточна функція розімкненої статичної системи
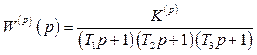 , (1.33)
, (1.33)
де Т1=1с; Т2=0,2с; Т3=0,05с.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.