Методичних вказівок до практичних занять з навчальної дисципліни „Теорія автоматичного керування”, страница 7

Записуємо систему рівнянь об’єкта

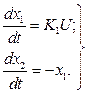,                                                       (4.2)

 де .

Накладаємо обмеження на керування

                                          (4.3)

Записуємо критерій оптимальності. За умовами задачі він має вигляд

.                        (4.4)

Ураховуючи (4.1), вводимо додаткову координату

,                                        (4.5)

звідки

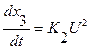.                                           (4.6)

Приєднуємо рівняння (4.6) до системи (4.2) і записуємо систему (4.2), ураховуючи (4.6).

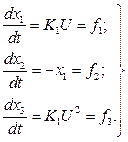.                            (4.7)

Складаємо гамільтоніан за умови, що

 

                       (4.8)

Від керуючої дії U(t) залежить тільки друга та четверта складова гамільтоніана, тому

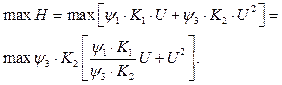                 (4.9)

Допоміжні функції  і оптимальне керування U⁰ відшукують із симетричної системи рівнянь Гамільтона.

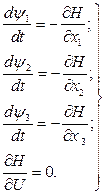                       ,                                        (4.10)

де

;                (4.11)

                                                                                (4.12)

                                                                (4.13)

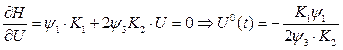               (4.14)

або

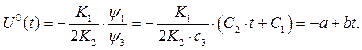       (4.15)

Відповідно (4.15) маємо лінійний закон з обмеженням.

Отже

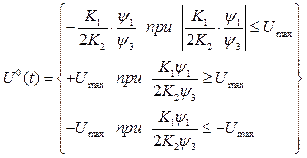.                      (4.16)

Якщо не ураховувати (4.1), що має місце, коли час керування дуже малий, то maxH досягається при  і закон керування може бути записаним таким чином

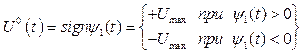.                   (4.17)

Відповідно (4.17) маємо релейний закон.

Функція (4.11) при любих співвідношеннях між С₁ і С₂ може змінювати свій знак тільки один раз і перетворюється в нуль при  .

Розв’язання 2 (за допомогою динамічного програмування).

Система рівнянь (4.7) і критерій оптимальності (4.4) незмінні.

Ураховуючи (4.7) і (4.4), складаємо рівняння Беллмана:

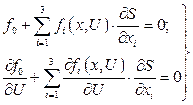                                  (4.18)

або

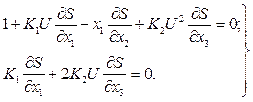                 (4.19)

Із другого рівняння системи (4.19) визначаємо

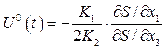.                                     (4.20)

Підставляємо (4.20) в перше рівняння системи (4.19) і маємо:

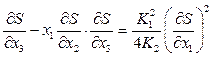.                         (4.21)

Вираз (4.21) – нелінійне диференціальне рівняння, де S – це функція Беллмана, яку для розв’язання цієї задачі можна подати в такому вигляді:

,                             (4.22)

 де

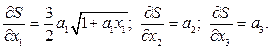                  (4.23)

Підставляємо (4.23) в (4.21) і маємо вираз

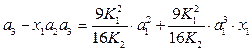,                      (4.24)

з якого визначаємо коефіцієнти а₁, а₂ і а₃, використовуючи такі рівняння

.

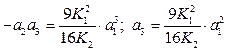Припустимо, що а₃=1, тоді

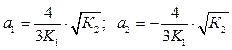                                 .                         (4.25)

Підставляємо (4.25) в (4.23) і далі (4.23) в (4.20) і одержуємо

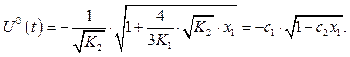             (4.26)

Порівнюючи (4.26) з (4.17) або (4.16), бачимо, що алгоритм керування не є функція часу, а є функція координати х₁ заданої системи електропривода, тобто маємо керування із зворотним зв’язком по координаті х₁(U⁰(x₁).

4.1.2 Визначити закон змінювання струму якоря двигуна постійного струму з незалежним збудженням, що забезпечує відпрацювання кутового переміщення  протягом мінімального часу Т. При обмежені струму якоря  і статичному моменті М_с=0.

При розв’язанні цієї задачи рекомендується використати [1]-С. 478-480.

4.1.3 Для об’єкта, що описується рівнянням

                                  (4.27)

знайти оптимальне керування U, при якому мінімізується функціонал

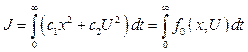.              (4.28)

4.1.4 Як необхідно керувати моментом двигуна постійного струму з незалежним збудженням, щоб повернути його вал на заданий кут  за мінімальний час?

Вважати початкову і конечну швидкості , момент статичного навантаження відсутній і . Розрахувати і зобразити М(t), (t), (t), якщо Р_н=2,4 кВт; _н=135 с^-1; J=0,2 кгм², , =30 рад. Всі значення величин приведені до вала двигуна.

При розв’язанні цієї задачі рекомендується використати [10] – С.101-102.

5. адаптивні системи автоматичного керування

                          (модуль 8)

                      Методичні вказівки

Адаптивна система автоматичного керування – це система, яка здатна в процесі виконання основної задачі керування за рахунок змінювання параметрів і структури регулятора поповнювати нестачу інформації про об’єкт керування і, діючі на його зовнішні збурення, поліпшувати якість свого функціонування.

Адаптивні системи звичайно поділяються на два класи: параметричні (самонастроювальні) і непараметричні (самоорганізуючі).

Історично першими адаптивними системами були системи екстремального керування, методи пошуку екстремуму яких поділяються на два види: детерміновані (методи градієнта, найбільш швидкого спуску, Гаусса-Зейделя) та випадкові (методи випадкових сліпих пошуків, статистичного градієнта та статистичного найбільш швидкого спуску).

Треба пам’ятати , що в багатьох випадках параметри об’єкта та зовнішні збурення змінюються в досить значних межах або взагалі інформація про властивості об’єкта неповна. Тому при проектуванні адаптивних систем виникає проблема ідентифікації об’єктів керування. Ціллю ідентифікації є визначення невідомих параметрів a_i і b_j об’єкта. Відомі різні методи ідентифікації, зокрема частотний метод і метод настроюваної моделі. Вимірюючи змінні стану настроюваної моделі можна таким чином реалізувати адаптивний спостерігач.

На відміну від системи адаптивного керування ідентифікацією за допомогою моделі, що настроюється, в системах з еталонною моделлю бажаний рух об’єкта задається моделлю, що є зразком або еталоном для об’єкта. Модель вибирається заздалегідь згідно з апріорною інформацією про вхідні дії. Завданням системи є настроювання параметрів основного контуру під параметри еталонної моделі.

У цьому розділі розглянуті задачі, що присвячені вивченню частотного метода ідентифікації об’єкта і керуванню об’єктом з еталонною моделлю.

При вирішенні задач цього розділу бажано повторити матеріал за літературою [1] – С. 519-538; [4] – С. 423-435; [7] – С. 164 – 193.

5.1 Практичне заняття 8.

5.1.1 Об’єкт другого порядку описується передаточною функцією

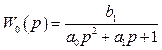,                                        (5.1)

параметри b₁, a₀, a₁якої невідомі. Для частот пробного сигналу  і  експериментально визначено значення дійсної та уявної частотних характеристик

U(1)=21,2: U(10)=-2,12; V(1)=-4,7; V(10) = -0,47.

За цими даними знайти параметри передаточної функції об’єкта.

Розв’язання. Виконавши підстановку  в (5.1), перейдемо до комплексної частотної передаточної функції

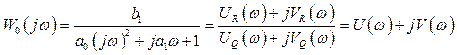       (5.2)

з якої дістанемо