Методичних вказівок до практичних занять з навчальної дисципліни „Теорія автоматичного керування”, страница 4

                              цифрової системи.

Записуємо ЛАЧХ по формулі  (2.26)

.      (2.37)

Вираз (2.37) відрізняється від (2.35) тільки останньою складовою. До частоти λ₀ вони збігаються, що відповідає теоремі Котельникова-Шеннона.

Збіг ЛАЧХ для дискретної передаточної функції і передаточної функції неперервної частини системи в зоні низьких частот дає можливість виконувати синтез керуючих пристроїв (цифрових регуляторів) відомими методами синтезу корегуючих пристроїв неперервних систем і використовувати розроблені для них номограми, графіки і таблиці.

Внаслідок синтезу методом ЛАЧХ знаходиться ЛАЧХ корегуючого пристрою L_K(λ) і за її виглядом визначається комплексна частотна функція W_К(jλ). Після цього виконується підстановка

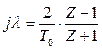,                                              (2.38)

і визначається дискретна передаточна функція W_К(Z), а потім різницеве рівняння корекції, що реалізується цифровим регулятором.

2.1.7 Записати решітчасту функцію f [n]і всі її різниці, що відповідають неперервній функції f (t)=5t. Побудувати графіки f [n] і Δf [n] при Т₀=1с.

2.1.8. Записати решітчасту функцію f [nТ₀], яка відповідає сумарному сигналу f (t), що складається з трьох складових, при наступних умовах:

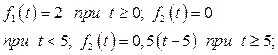
Визначити значення функції при n=7 і Т₀=2,5с. Побудувати решітчасту функцію f [nТ₀].

2.1.9 Визначити стійкість замкненої імпульсної системи, характеристичне рівняння якої має вигляд

.                                                           (2.39)

2.1.10 Структурна схема цифрового регулювання швидкості двигуна постійного струму наведена на рисунку 2.3.

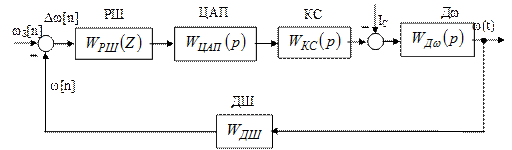
Рисунок 2.3 – Структурна схема

На рисунку 2.3 позначено: РШ– дискретний регулятор на базі мікроЕОМ; ЦАП – цифро-аналоговий перетворювач у вигляді ідеального імпульсного елемента с періодом квантування Т₀ і фіксатора нульового порядку; КС– контур струму, настроєний на технічний оптимум; Д_ω– електромеханічна частина двигуна постійного струму; ДШ – імпульсний давач швидкості.

Елементи схеми на рисунку 2.3 характеризуються передаточними функціями відповідно

,

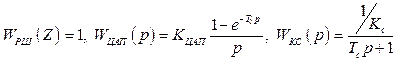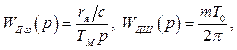
де К_с=1 В/А, Т_С=0,1с, К_ЦАП=3, r_Я=0,2Ом, с=4,3 , Т_м=0,3с, m=600 імпульсів за оберт.

Визначити чи стійка система при Т₀=Т_С і Т₀=4Т_С.

При вирішенні цієї задачі рекомендується використати [1]– C.450-453.

2.1.11 Для імпульсного фільтра, наведеного на рисунку 2.4, побудувати L(λ) і φ(λ), де 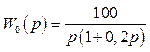, період квантування Т₀=0,05с, шпаруватість імпульсів γ=0,1с.

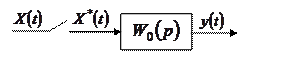
Рисунок 2.4 – Схема імпульсного фільтра

2.1.12 Передаточна функція замкненої імпульсної системи

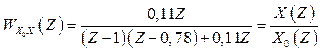.                      (2.40)

Визначити різницеве рівняння імпульсної системи, яке зв’язує вхідну і вихідну координати імпульсної системи. Для вирішення цієї задачі рекомендується використати [4]– С.293.

             2.2 Практичне заняття 4    Якість та корекція ДСАК

2.2.1 Імпульсна система складається з ключа (ідеального імпульсного елемента), фіксатора (екстраполятора нульового порядку) та ідеальної інтегруючої ланки (об’єкта) з передаточною функцією

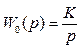                                       .                                        (2.41)

Скласти алгоритмічну структурну схему та одержати:

1)  дискретну передаточну функцію розімкненого контуру регулювання ;

2)  дискретну передаточну функцію по завдаючій дії  та по похибці . Визначити усталену похибку при .

Розв’язання. Алгоритмічна структурна схема за умовами задачі має вигляд

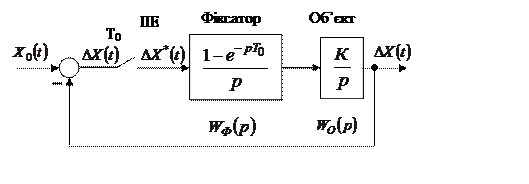
Рисунок 2.5 –Структурна схема імпульсної системи

У відповідності з рисунком 2.5

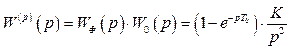.                              (2.42)

Дискретна передаточна функція розімкненого контуру

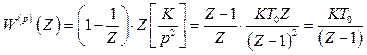 ,                     (2.43)

де .

Дискретна передаточна функція замкненої системи по завдаючій дії

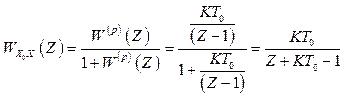;          (2.44)

по похибці

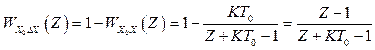      .           (2.45)

Усталена похибка по завиваючій дії обчислюється по формулі

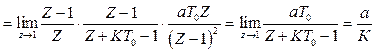                     .   (2.46)

2.2.2 Дискретна передаточна функція розімкненого контуру імпульсної системи

                                        (2.47)

Побудувати перехідні процеси h[nT₀] і визначити основні показники якості перехідного процесу при

1) КТ₀=0,5;  2) КТ₀=1;  3) КТ₀=1,5.

При якому значенні КТ₀ процес оптимальний?

Розв’язання. Якість перехідних процесів імпульсних систем оцінюється такими самими показниками, як і неперервних. Найважливішими з них є тривалість перехідного процесу t_П і максимальне відхилення  регульованої величини від усталеного значення.

Послідовність знаходження h(t) наступна:

.        (2.48)

Відповідно (2.48) обчислюємо

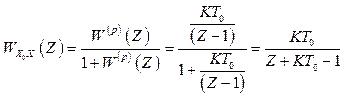,                 (2.49)

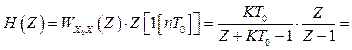
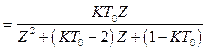.                              (2.50)

Записуємо вирази H(Z) для КТ₀=0,5; КТ₀=1; КТ₀=1,5.

;

;

.

Розкладемо вирази ,  і  в степені ряди по убиваючим степеням.

При КТ₀=0,5:

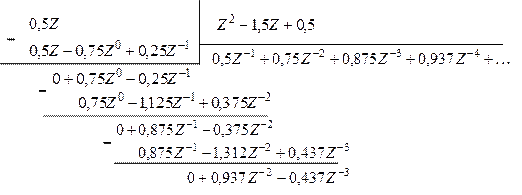
При КТ₀=1:

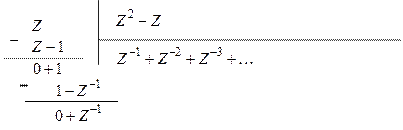
Одержуємо

      (2.51)

                                          (2.52)

і аналогічно

       (2.53)

Коефіцієнти рядів (2.51)÷(2.53) відповідають ординатам перехідних функцій h₁(t), h₂(t) і h₃(t), які наведені на рисунку2.6.

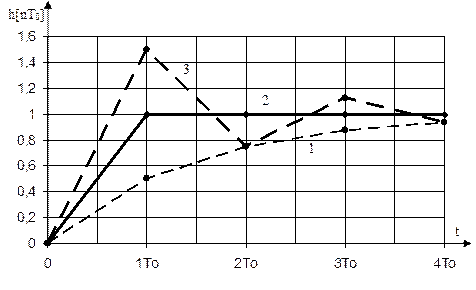
Рисунок 2.6 – Перехідні функції імпульсної системи

Показники якості перехідних процесів наступні:

Оптимальним по швидкодії є процес 2.

2.2.3 Передаточна функція розімкненої імпульсної системи має вигляд

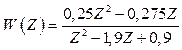  .                                                    (2.54)

Визначити перші два коефіцієнти похибок С₀ і С₁ при Т₀=0,1с.

Розв’язання. Записуємо передаточну функцію замкненої системи відносно похибки

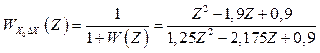.                      (2.55)

Коефіцієнт похибки

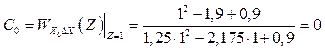.                     (2.56)

Для визначення коефіцієнта похибки С₁ перепишемо передаточну функцію (2.55), у вигляді

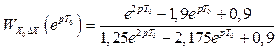                                 (  2.57)

Продифереціюємо вираз (2.57) по змінній р

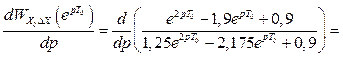
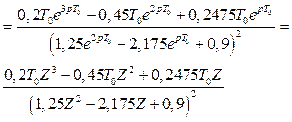             .                               (2.58)

При Т₀=0,1с

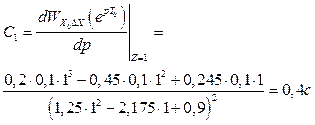                                       (2.59)

2.2.4 Передаточна функція розімкненої системи

.                                                     (2.60)

Визначити, при яких значеннях коефіцієнта К імпульсна система стійка у замкненому стані.

2.2.5 Передаточна функція замкненої системи

                                                      (2.61)

Визначити перші два коефіцієнти похибки С₀ і С₁ при Т₀=0,1с.

2.2.6 Для одноконтурної системи з ЦОМ передаточна функція дискретної частини  ,  а неперервної -   .

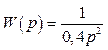Визначити, при яких значеннях періоду дискретності Т₀ замкнута система стійка. Квантуванням за рівнем і запізнюванням ЦОМ знехтувати.