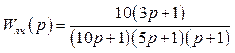Методичних вказівок до практичних занять з навчальної дисципліни „Теорія автоматичного керування”, страница 6

, а .

3.1.4 Типова структурна схема нелінійної системи наведена на рисунком 3.4

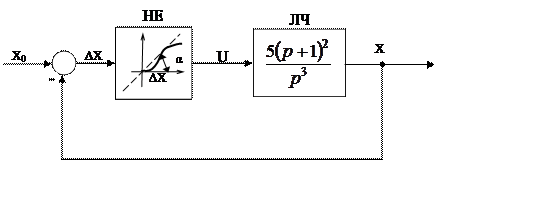
Рисунок 3.4 – Структурна схема нелінійної системи

Визначити умови абсолютної стійкості, тобто  за рисунком. 3.4.

3.1.5. Визначити характер автоколивань суттєво нелінійної системи за структурною схемою рисунку 3.3, а також параметри автоколивань, якщо передаточна функція лінійної частини

,

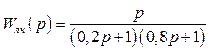а нелінійна ланка має релейну характеристику з с=1,6 , b=0.

3.1.6 Типова структурна схема нелінійної системи наведена на рисунку3.5

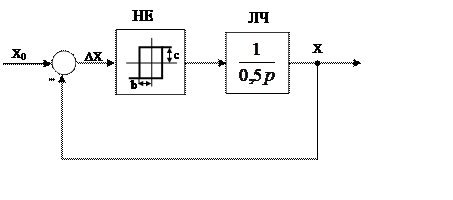
        Рисунок 3.5 – Структурна схема нелінійної системи.

Дослідити режим автоколивань.

3.2 Практичне заняття 6

Якість і корекція нелінійних САК

3.2.1 Покажіть, що у нелінійній системі, структурна схема якої наведена на рисунку 3.6, призначеннях параметрів лінійної частини К=0,82с^-1 і Т=0,05 с та статичній характеристиці нелінійного елемента, для якої b=0,25, c=110 , виникає режим автоколивань з амплітудою U_ma=2,86 і частотою . Для доказу скористайтеся критерієм Найквіста.

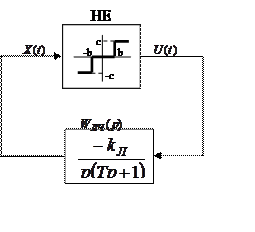
Рисунок 3.6 - Структурна схема нелінійної системи.

Розв’язання. Відповідно критерію Найквіста лінійна система знаходиться на межі стійкості, якщо АФХ розімкненої системи проходить через критичну точку з координатами [-1,j0], тобто рівняння, що відповідає незатухаючим коливанням, має вигляд

.                                            (3.21)

Для нелінійної системи це рівняння має вигляд

                               (3.22)

або

,                                (3.23)

або

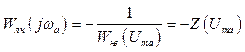,                         (3.24)

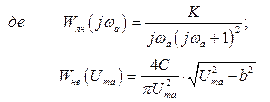
при .

В одній системі координат будуємо  і

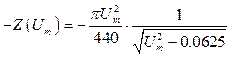.                            (3.25)

В точках перетину характеристик  і  виконується рівняння (3.24). Ці точки визначають параметри автоколивань  на кривій  і  на кривій .

Спочатку будуємо криву , задаючись значеннями  від .

У даному випадку цей годограф збігається з негативною дійсною піввіссю і має верхню і нижню вітки відносно осі. Мінімальне значення модуля

.                 (3.26)

Для побудови  можна використати вирази

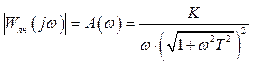                                    (3.27)

та .                                                  (3.28)

У цій задачі нема необхідності будувати всю криву АФХ. Достатньо знайти точку перетину характеристики  з негативною дійсною піввіссю. Перетин зчинеться на частоті  при

,                                  (3.29)

звідки знаходимо

                              .                                     (3.30)

Підставляємо значення для  в вираз (3.27) і обчислюємо

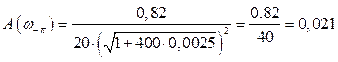.               (3.31)

Частота  задовольняє двом значенням :  та , які відповідають точкам М₁ і М₂ (рис. 3.7). Для точки М₂ =2,86. В цій точці у відповідності з критерієм Найквіста виникає режим автоколивань з =20с^-1 і =2,86.

Перевірка.

В точці М₂:

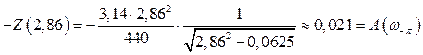
Рисунок 3.7 – Характеристики

3.2.2 Покажіть і докажіть, яку керуючу ланку потрібно внести в лінійну частину суттєво нелінійної системи в умовах задачі 3.2.1 для того, щоб зірвати автоколивальний режим. Для доказу скористайтесь критерієм Найквіста.

3.2.3 Побудуйте сім’ю фазових траєкторій системи, структурна схема якої наведена на рисунку 3.8.

Покажіть ту частину лінії перемикання, де виникає ковзний режим.

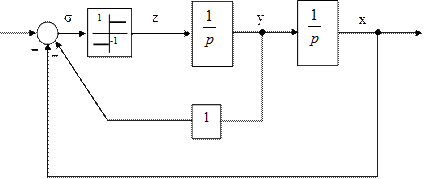
          Рисунок 3.8 – Структурна схема нелінійної системи

3.2.4 Дослідити стійкість стану рівноваги нелінійної системи, структурна схема якої наведена на рисунку 3.9. Числові дані такі: К₁=10с^-1; Т₁=0,1с; а₁=0,1; а₂=0,3; К=tg=5

     Рисунок 3.9 – Структурна схема нелінійної системи.

4. Методи синтезу оптимальних систем

автоматичного керування

(модуль 7)

Методичні вказівки

Система автоматичного керування називається оптимальною, якщо в ній тим чи іншим способом забезпечується найкраще значення критерія оптимальності. Звичайно критерії оптимальності це інтегральні квадратичні функціонали від однієї або кількох функцій. Розробка оптимальних систем, тобто визначення такої керуючої функції, яка забезпечує мінімум відповідного функціоналу, це задача варіаційного числення. Методи варіаційного числення можна умовно розділити на класичні (Ейлера, Якобі, Вейєрштрасса) і некласичні (сучасні – принцип максимуму Понтрягіна і метод динамічного програмування Беллмана).

Класичні методи доцільно застосовувати в задачах, що не мають обмежень, тобто у випадках, коли розглядаються малі відхилення змінних стану і керувань від усталених значень.

Некласичні методи розроблені саме для розв’язання задач оптимального керування з врахуванням обмежень керувань і змінних стану. Вони оперують з широким класом функцій керування, пристосовані також для використання обчислювальної техніки.

Для синтезу систем оптимального керування електроприводами найчастіше використовуються сучасні методи варіаційного числення. Саме цим методам і присвячені задачі, які пропонуються у цьому розділі.

Треба пам’ятати, що при синтезі оптимальних систем автоматичного керування за допомогою принципу максимуму функції керуючої величини є кусково-безперервними, а теорема про n-інтервали дійсна лише для систем, характеристичне рівняння яких має дійсні корені. Крім того, найскладнішою частиною при розв’язанні цих задач є розрахунок часу окремих інтервалів, які знаходяться завдяки заданим граничним значенням вихідних координат.

Метод динамічного програмування рівноцінний принципу максимуму Понтрягіна, але дозволяє одержати керуючу координату як функцію змінних стану. За допомогою цього методу можна провести також аналітичне конструювання оптимальних регуляторів (АКОР). Одним з методів АКОР, що базується на застосуванні методу динамічного програмування для певного класу систем, є метод О.М. Льотова.

При вирішенні задач цього розділу бажано повторити матеріал за літературою: [1] – С. 472–492; [2] – С. 365– 409;[4] – С.394– 403; [7] – С. 7–67.

4.1 Практичне заняття 7

4.1.1 Для об’єкта керування, принципова схема якого наведена на рисунку 4.1, треба знайти алгоритм керування (U), який переводить систему з положення Х₁=0, Х₂=Х_2П при t=0 в положення Х₁=0, Х₂=0 за мінімальний час τ при обмеженні витрат енергії на керування.

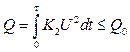.                                    (4.1)

Розв’язання 1 (за допомогою принципу максимуму).

Принциповій схемі об’єкта (рис. 4.1) відповідає структурна схема, яка наведена на рисунку 4.2.

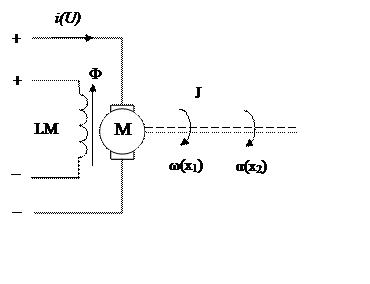
Рисунок 4.1 – Принципова схема об’єкта керування.

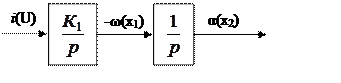
Рисунок 4.2 –Структурна схема об’єкта

Вирішуємо задачу в такій послідовності.