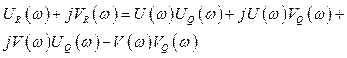Методичних вказівок до практичних занять з навчальної дисципліни „Теорія автоматичного керування”, страница 8

.               (5.3)

Порівнявши дійсні та уявні частини виразу (5.3), дістанемо два рівняння

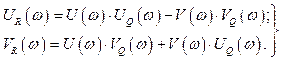                    (5.4)

Для заданої передаточної функції об’єкта ; ; ; , тому система рівнянь (5.4) для частот ₁ і ₂ матиме вигляд

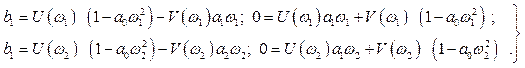                                                                                                                  (5.5)

або після підстановки числових значень

                                            (5.6)

                                             (5.7)

                                     (5.8)

.                                   (5.9)

Рівняння (5.7) і (5.9) не залежать від . Розв’язавши їх знайдемо =0,1; =0,2. Підставивши ці значення в будь-яке рівняння (5.6) або (5.8), визначаємо =20.

5.1.2 Функціональна схема одновимірної адаптивної системи з еталонною моделлю наведена на рисунку5.1

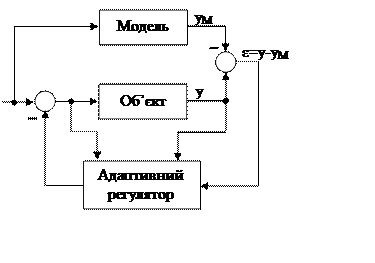
Рисунок 5.1 – Функціональна схема адаптивної системи.

Для випадку коли передаточна функція моделі

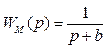,                                          (5.10)

а об’єкт має передаточну функцію

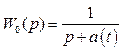                                                                       (5.11)

і охоплений жорстким зворотним зв’язком (рис. 5.2)

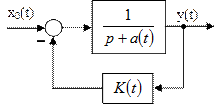
               Рисунок 5.2 –Структурна схема об’єкта

визначити закон змінювання коефіцієнта зворотного зв’язку  в основному контурі, який би забезпечив збіг передаточної функції об’єкта з регулятором з передаточною функцією моделі.

Розв’язання. Вважаємо, що змінний параметр об’єкта має вигляд

    ,                     (5.12)

 де =const, а настроюваний коефіцієнт зворотного зв’язку – вигляд

                                       .                           (5.13)

        У цьому разі передаточна функція основного контуру (об’єкта, охопленого зворотним зв’язком) записується так:

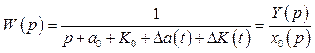,                     (5.14)

 де

Передаточним функціям об’єкта (5.14) і моделі (5.10) відповідають диференціальні рівняння, які мають вигляд

                            (5.15)

                                          (5.16)

Беручи до уваги, що  та  віднімемо вираз (5.16) від (5.15).

Після віднімання дістаємо рівняння відносно похибки розузгодження рухів системи та еталонної моделі

                        (5.17)

 де

                                    (5.18)

Є параметричне розузгодження.

При =0 і b>0  асимптотичне прямує до нуля.

 Припустимо що коефіцієнт К змінюється за допомогою виконавчого пристрою і що виконавчий пристрій становить інтегруючу ланку, тоді

                                        (5.19)

 де  - шуканий закон керування в контурі самонастроювань-ня.

Запишемо рівняння (5.17) у вигляді

                                      (5.20)

Продиференцюємо (5.18) і, враховуючи (5.19), дістанемо

                        .                                  (5.21)

Шуканий закон керування  в контурі самонастроювання можна визначити з умов здійснення бажаного руху зображуючої точки по площині  за рівняннями (5.20) і (5.21).

Для цього скористаємося прямим методом Ляпунова, взявши визначено-додатну функцію у вигляді

                                               (5.22)

 де c>0.

Вважатимемо також, що параметри об’єкта за час перестроювання коефіцієнта К не змінюються, тобто . Тоді повна похід-на функція Ляпунова буде мати вигляд

              (5.23)

або, з врахуванням рівнянь (5.20) і (5.21), – у вигляді

.                    (5.24)

Якщо взяти  ,

              де  - алгоритм самонастроювання, то вираз (5.24) перство-рюється в вираз (5.25)

.                                   (5.25)

Це означає, що нульовий розв’язок  системи рівнянь (5.20) і (5.21) є стійким.

Отже, закон змінювання коефіцієнта зворотного зв’язку в основному контурі є наступним

                                        (5.26)

 де                                                                 (5.27)

Структурна схема цієї адаптивної системи з еталонною моделлю і синтезованим законом змінювання коефіцієнта зворотного зв’язку в основному контурі наведена на рисунку 5.3.

5.1.3 За умовами задачі 5.1.1 визначити параметри об’єкта, якщо для частот пробного сигналу =10 с^-1 і ₂ = 30 с^-1 експериментально визначено значення дійсної та умовної частотних характеристик

5.1.4 Структурна схема одновимірної адаптивної системи з еталонною моделлю наведена на рисунку 5.4

Визначити алгоритм перестроювання коефіцієнта підсилення К_с за умови стійкості процесу в системі з еталонною моделлю для компенсації змінення коефіцієнта передачі об’єкта К(t).Побудувати структурну схему синтезованої адаптивної системи.

Указання. Взяти функцію Ляпунова у вигляді [12] – С. 451

                                  (5.28)

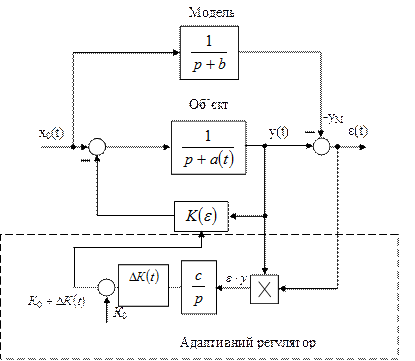
            Рисунок 5.3 – Структурна схема адаптивної системи

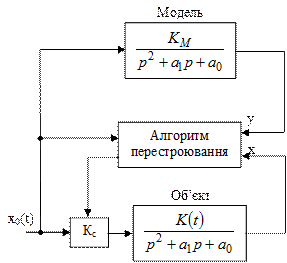
Рисунок 5.4 – Структурна схема адаптивної системи

Список літератури

1.  Попович М.Г., Ковальчук О.В. Теорія автоматичного керування. – К.:Либідь, 1997. – 554 с.

2.  Лукас В.А. Теория автоматического управления. – М.: Недра, 1990. – 416 с.

3.  Методические указания к домашним заданиям по курсу «Теория автоматического управления» (для студентов специальности 7.092203) / Сост.: Н.Н. Сергиенко – Алчевск: ДГМИ, 2003. – 54с.

4.  Сборник задач по теории автоматического регулирования и управления / Под ред. В.А. Бесекерского. – М.: Надра, 1978. – 512 с.

5.  Расчёт автоматических систем: Учебное пособие / Под ред. А.В. Фатеева. – М.: Высш. шк., 1973 – 336 с.

6.  Куо Б. Теория и проектирование цифровых систем управления: - М.: Машиностроение, 1986. – 448 с.

7.  Александров А.Г. Оптимальные и адаптивные системы: Учеб. пособие для вузов по спец. «Автоматика и управление в техн. системах».– М.:Высш. шк., 1989. – 263 с.

8.  Теория автоматического управления: 4.2. Учебник для вузов./Под ред. А.В.Нетушила. – М.:Высш. шк., 1972 – 432 с.

9.  Теория автоматического управления: Учебник для вузов / Под ред А.В.Нетушила. – 2-е изд., доп. и перераб. – М.: Высш. шк., 1976. – 400 с.

10. Герасимяк Р.П. Теорія автоматичного керування. Збірник задач: Навч. посібн. – Одеса: Наука і техніка, 2003. – 108 с.

11. Зайцев Г.Ф. Теория автоматического управления и регулирования. – 2-е изд., доп. и перераб. – К.:Высш. шк.,1988. – 431 с.

12. Топчеев  Ю.И , Цыпляков А.П. Задачник по теории автоматического регулирования .Учебное пособие для вузов .М. “Машиностроение”, 1977.-592с.