Методичних вказівок до практичних занять з навчальної дисципліни „Теорія автоматичного керування”, страница 5

2.2.7 Дискретна передаточна функція розімкненого контуру імпульсної системи

.                                              (2.62)

Побудувати перехідну функцію h[nT₀] і визначити основні показники перехідного процесу при Т₀=0,1с.

3. Математичні моделі, стійкість, якість та корекція нелінійних систем автоматичного керування (модуль 6)

Методичні вказівки.

Усі реальні системи автоматичного керування (САК) електроприводами – нелінійні. Однак їх можна поділити на дві групи: несуттєво нелінійні і суттєво нелінійні.

Треба пам’ятати, що несуттєво нелінійні системи можна лінеаризувати і для їх аналізу і синтезу застосувати теорію лінійних САК і їх математичні моделі, але лише при досить малих відхиленнях від режиму, що досліджується.

Проте існує велика кількість САК, у яких суттєво нелінійні ланки є частиною об’єкта (підсилювачі з насиченням, елементи механічних передач з люфтами і сухим тертям та інші), або нелінійні ланки (релейні елементи, логічні перемикаючі пристрої) упроваджуються спеціально з метою забезпечення таких властивостей систем, що принципово не можуть бути досягнуті в лінійних системах.

Аналіз і синтез суттєво нелінійних САК набагато складніший і ось чому:

1)  стійкість нелінійних систем на відміну від лінійних залежить від величини і місця прикладання зовнішньої дії;

2)  характер перехідного процесу змінюється при зміні величини зовнішньої дії;

3)    в нелінійних системах спостерігаються режими, які неможливі в лінійних системах, зокрема режим автоколивань.

Загальна теорія аналізу і синтезу суттєво нелінійних систем, на відміну від лінійних, відсутня. Усе це потребує застосування спеціальних точних і наближених математичних моделей для аналізу стійкості, якості і синтезу нелінійних систем.

При математичному описуванні суттєво нелінійних систем несуттєві нелінійності лінеаризують, а суттєві спрощують, зводячи їх до типових. У цьому разі математична модель суттєво нелінійної САК становить структурну схему, що складається з лінійних (лінеаризованих) ланок і ланок з типовими суттєво нелінійними характеристиками.

У даному розділі наведені задачі, в яких використовується частотний метод абсолютної стійкості (метод В.М. Попова), метод гармонічної лінеаризації і метод вібраційної лінеаризації в ковзному режимі.

Дослідження нелінійних САК за допомогою цих методів, як і в більшості інших, орієнтовано на структурні схеми, що складаються з однієї безінерційної суттєво нелінійної ланки і лінійної частини з передаточною функцією W_лч(р). Зовнішні дії перенесені на вхід нелінійної ланки.

При вирішенні задач цього розділу рекомендується повторити матеріал за літературою [1] – С. 336-341, 344-362; [2] – С. 313-330;[4] – С. 329-335, 337-350;[11] – С. 312, 315-329, а також конспект лекцій.

3.1 Практичне заняття 5.  Математичні моделі і стійкість

нелінійних САК

3.1.1 Покажіть, що нелінійна автоматична система, структурна схема якої наведена на рисунку 3.1, при значеннях параметрів лінійної частини К_Л=1 і Т=1с та статичній характеристиці суттєво нелінійного елемента з параметрами с=20 і b=4 буде абсолютно стійкою. Знайдіть також критичне значення коефіцієнта передачі  К_кр = К_л К_не

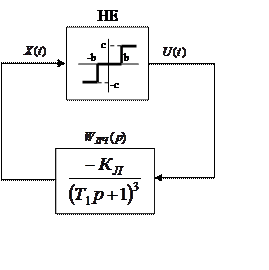
           Рисунок 3.1 – Структурна схема нелінійної системи

Розв’язання. Передаточна функція лінійної частини нелінійної системи

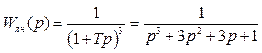.                        (3.1)

Перетворимо вираз 3.1 в W_лч(j) і подамо у вигляді

                 ,                          (3.2)

де

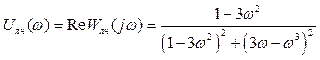            ,          (3.3)

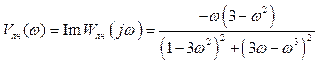,                      (3.4)

Введемо поняття видозміненої (модифікованої) частотної характеристики лінійної частини системи або кривої Попова.

Вираз цієї характеристики

,                                                  (3.5)

 де

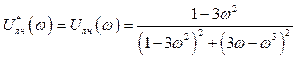,                           (3.6)

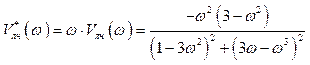,                       (3.7)

Визначаємо також коефіцієнт передачі нелінійного елемента

.                                                                    (3.8)

По виразам (3.6) і (3.7) обчислюємо і будуємо амплітудно-фазову характеристику . Дані для побудови  наведені в таблиці 3.1, а  і прямі Попова на рисунку 3.2

Таблиця 3.1 – Дані для побудови  

	0	1	1,25	1,5	1,75	2,0
	1	-0,25	-0,21	-0,15	-0,12	-0,09	0
	0	-0,25	-0,13	-0,048	-0,02	+0,032	0

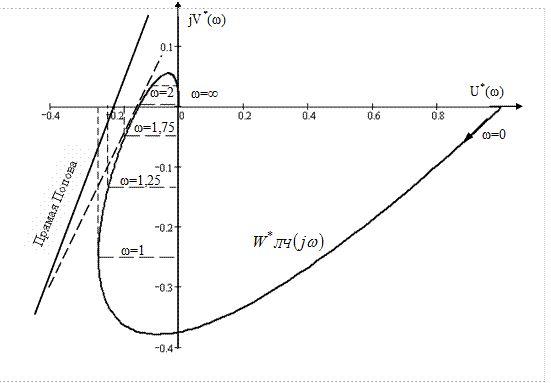
Рисунок 3.2 – АФХ і прямі Попова

Згідно рисунку 3.2 нелінійна система абсолютно стійка, тому що в площині  можна провести пряму Попова через точку з координатами 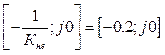 так, щоб характеристика  знаходилась праворуч від неї.

Щоб знайти критичний коефіцієнт передачі К_кр необхідно пряму Попова перемістити таким чином , щоб вона торкнулася  на осі  (пунктирна пряма). На рисунку 3.2 точкою дотику є точка з координатами  . Отже

.3.1.2 Покажіть, що у суттєво нелінійній системі, структурна схема якої наведена на рисунку 3.3, при значеннях параметрів лінійної частини та статичній характеристиці нелінійного елемента з b=0,25, с=110 виникає режим автоколивань з амплітудою  і частотою .

Для доказу використайте критерій Михайлова.

Розв’язання. Передаточна функція гармонічно лінеаризованого нелінійного елемента

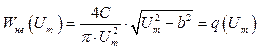;                                    (3.9)

q₁(U_m)=0; U_mb.

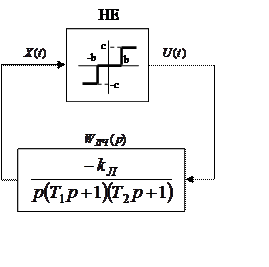
Рисунок 3.3 – Структурна схема нелінійної системи.

Враховуючи (3.9), записуємо характеристичний поліном замкненої системи.

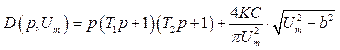                (3.10)

або

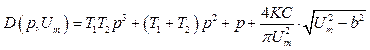.       (3.11)

Після підставлення в (3.11) р= маємо:

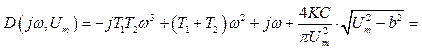
,                                                                  (3.12)

 де

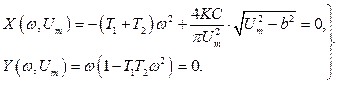                (3.13)

Із другого рівняння системи (3.13) при  знаходимо:

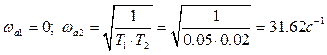.       (3.14)

Значення  підставляємо в перше рівняння системи (3.13) і після його перетворення одержуємо вираз

,             (3.15)

звідки =15,95 , а =0,0627

або

.                   (3.16)

Перевіряємо автоколивання на стійкість по формулі:

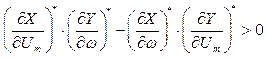,                                (3.17)

 де

 ,

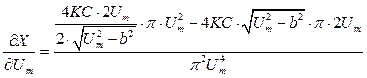=0, .

Зважаючи на те, що =0, перевіряємо тільки умову

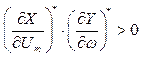.                                                             (3.18)

При підстановці в вираз (3.18)  і  
маємо

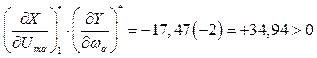                      (3.19)

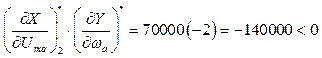                    (3.20)

Порівнюючи 3.19 і 3.20 робимо висновок: автоколивання стійкі при .

3.1.3 Перевірити, чи виконується умова абсолютної стійкості нелінійної системи за структурною схемою рисунку 3.1, якщо