Визначити наближеним частотним методом коефіцієнт підсилення К(р), щоб показник коливальності М замкненої системи мав значення 1,4. Розрахувати також коефіцієнт демпфування ξ, приблизні значення перерегулювання σ і часу перехідного процесу tр.
1.1.5 Передаточна функція розімкненої системи з астатизмом першого порядку
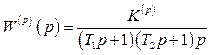 , (1.34)
, (1.34)
де Т1=0,011с; Т2=0,03с.
Визначити за допомогою наближеної моделі значення коефіцієнта демпфування ξ замкненої системи, який забезпечує мінімум поліпшеної інтегральної квадратичної оцінки
![]() , (1.35)
, (1.35)
а також значення коефіцієнта підсилення К(р).
1.1.6 Передаточна функція розімкненої астатичної системи
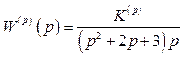 . (1.36)
. (1.36)
Знайти значення коефіцієнта підсилення К(р) за умови стійкості замкненої системи, а також за умови необхідності, щоб за час перехідного процесу замкненої системи tр =5с, відхилення регульованої величини не перевищувало Δ=5% від початкового значення.
Для вирішення цієї задачі рекомендується використати [1]–С.200–204.
1.2 Практичне заняття 2. Синтез САК
1.2.1 В системі „тиристорний перетворювач-двигун постійного струму з незалежним збудженням „ (ТП-Д) забезпечте інваріантність по збуренню (моменту статичного навантаження). Нарисуйте розгорнуту алгоритмічну структурну схему системи ТП-Д з компенсаційним каналом по збуренню та синтезуйте передаточну функцію корегуючої ланки у компенсаційному каналі.
Розв’язання. Розгорнута алгоритмічна структурна схема системи ТП-Д наведена на рисунку1.1.
Умова інваріантності по збуренню:
![]() , (1.37)
, (1.37)
звідки
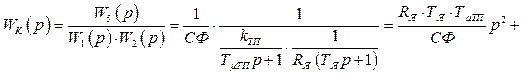
![]() . (1.38)
. (1.38)
Повна (абсолютна інваріантність наступає при
![]() ;
; ![]() ;
; ![]() .(1.39)
.(1.39)
1.2.2 За заданими тривалістю перехідного процесу tр=0,1с та перерегулюванням σmax%=25% визначити передаточну функцію і параметри послідовного корегуючого пристрою для замкненої астатичної системи, передаточна функція якої у розімкненому нескорегованому стані
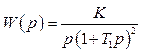 , (1.40)
, (1.40)
де К=80с-1; Т1=0,0125с.
|
|
Рисунок 1.1 – Розгорнута алгоритмічна структурна схема системи ТП- Д з компенсаційним каналом по збуренню |
Розв’язання. Синтез послідовного корегуючого пристрою будемо вести по методу логарифмічних амплітудно-частотних характеристик (ЛАЧХ) розімкненої системи, використовуючи для цього вихідну і бажану ЛАЧХ системи.
Спочатку по (1.40) записуємо вираз для побудови вихідної ЛАЧХ
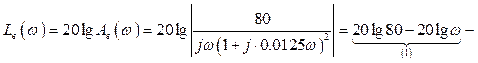
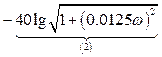 ,
(1.41)
,
(1.41)
де ![]() і
і ![]() –
асимптоти вихідної ЛАЧХ, які сполучаються між собою на частоті
–
асимптоти вихідної ЛАЧХ, які сполучаються між собою на частоті ![]() . Вихідна ЛАЧХ наведена на рисунку
1.2 і відноситься до типу „-1-3”.
. Вихідна ЛАЧХ наведена на рисунку
1.2 і відноситься до типу „-1-3”.
Далі по виду вихідної ЛАЧХ нескорегованої системи, а також в залежності від вимог замовника системи керування вибираємо по методу Санковського – Сігалова [1]–С.269, таблиці6.2 асимптотичну бажану ЛАЧХ типу „1–2–1–2”. Але, з точки зору простості технічної реалізації корегуючого пристрою, вибираємо бажану ЛАЧХ типу „1–2–1–3”.
Бажана асимптотична
ЛАЧХ наведена на рисунку 1.2. Вона будується по частотам ![]() ,
, ![]() і
і![]() .
.
Частоту зрізу ![]() бажаної ЛАЧХ відшукуємо по [3] – С.62,
рисунок Б2б для σmax%=25% і tр=0,1с
бажаної ЛАЧХ відшукуємо по [3] – С.62,
рисунок Б2б для σmax%=25% і tр=0,1с
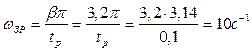 . (1.42)
. (1.42)
Частоти, що обмежують середньо-частотну асимптоту бажаної ЛАЧХ ліворуч і праворуч, обчислюємо, виходячи з таких наближених рівностей
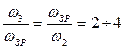 (гранично до 10), (1.43)
(гранично до 10), (1.43)
звідки (при співвідношенні частот, яке дорівнює 8) маємо
![]() ;
;
![]() . (1.44)
. (1.44)
По рисунку 1.2 записуємо вираз для Lδ(ω)
![]()
![]() ,
(1.45)
,
(1.45)
де ![]() ,
, ![]() ,
,
![]() .
.
ЛАЧХ корегуючого пристрою
![]()
![]()
![]() ,
(1.46)
,
(1.46)
що відповідає передаточній функції [1]-с.254, таблиці 6.1 пружної ланки з перевагою властивостей інтегруючої ланки
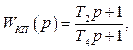 (1.47)
(1.47)
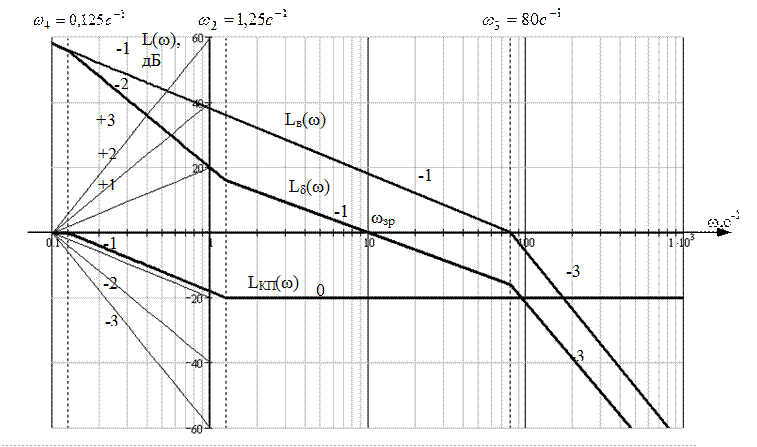
Рисунок 1.2 – Вихідна LВ(ω), бажана Lδ(ω) і ЛАЧХ корегуючого пристрою LКП(ω).
де Т4=8с, Т2=0,8с.
Передаточна функція (1.47) може бути реалізована за допомогою пасивного чотирьохполюсника, електрична схема якого має вигляд
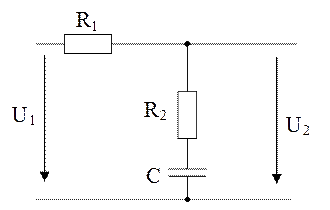
Рисунок 1.3 – Електрична схема корегуючої ланки
Параметри схеми обчислюються по формулам:
![]() ;
; ![]() . (1.48)
. (1.48)
Для визначення параметрів R1, R2 і C необхідно значення одного із параметрів задати і через нього знаходити значення інших параметрів.
1.2.3 За умови задачі 1.2.2, але для бажаної ЛАЧХ типу „–1–2–1–2” побудувати ЛАЧХ корегуючої ланки, вибрати її схему і розрахувати параметри схеми.
1.2.4 Двигун постійного струму
підключено до керуючого перетворювача (система ТП-Д). Знайти параметри
регулятора струму при настройці контуру струму на модульний оптимум без врахування
внутрішнього звовротнього зв’язку за
швидкістю. Зобразити структурну схему. Мала стала часу керуючого перетворювача
КП– ТμП=0,01с., коефіцієнт давача струму КС=0,14![]() . Інші дані двигуна і перетворювача
такі:
. Інші дані двигуна і перетворювача
такі:
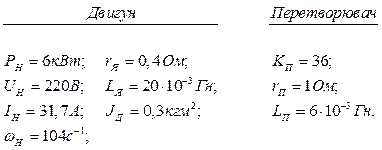
1.2.5 Для слідкуючої системи з комбінованим керуванням, алгоритмічна структурна схема якої наведена на рисунку1.4, знайдіть передаточну функцію коригуючого пристрою Wкп(р), що забезпечує повну інваріантність системи при любому характерові завдаючої дії. З якою фундаментальною суперечністю в теорії автоматичного керування Ви зіткнетесь, вирішуючи проблему інваріантності системи?
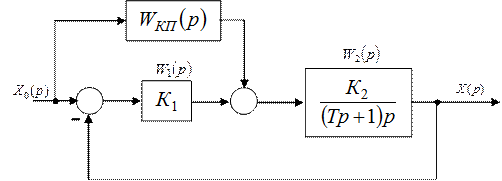
Рисунок 1.4 – Алгоритмічна структурна схема
1.2.6 При оптимізації типової
одноконтурної системи на модульний оптимум з передаточною функцією об’єкта
регулювання ![]() синтезується регулятор з
пропорційно-інтегральним законом керування. Обґрунтуйте, яким повинен бути закон
керування регулятора при таких передаточних функціях об’єкта:
синтезується регулятор з
пропорційно-інтегральним законом керування. Обґрунтуйте, яким повинен бути закон
керування регулятора при таких передаточних функціях об’єкта:
![]() .
.
1.2.7 За заданими показниками якості обрати послідовний коригуючий пристрій і розрахувати його параметри для САК, передаточна функція якої в розімкненому стані
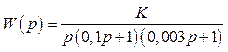 (1.48)
(1.48)
Коефіцієнт
швидкісної похибки С1=0,004 с, тривалість перехідного процесу при
стрибку завдання має бути ![]() , перерегулювання
, перерегулювання ![]()
2 Математичні моделі, стійкість, якість
та корекція дискретних систем автоматичного керування (ДСАК)
(модуль 5)
Методичні вказівки
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.