Методичних вказівок до практичних занять з навчальної дисципліни „Теорія автоматичного керування”, страница 3

Дискретні (імпульсні і особливо цифрової) системи набувають за останні роки все більш широкого розповсюдження. Цифрові системи будуються на базі комплексу засобів обчислювальної техніки: цифрової обчислювальної машини (ЦОМ), аналого-цифрового (АЦП) і цифро-аналогового (ЦАП) перетворювачів для випадку состиковки ЦОМ з аналоговими сигналами. Треба пам’ятати, що дискретна природа ЦОМ обумовила наявність двох процесів в системах цифрового керування: квантування сигналу за часом і рівнем. Квантування за часом робить цифрову систему дискретною, а квантування за рівнем – нелінійною. Звичайно кількість ступенів квантування за рівнем велико, тому впливом квантування за рівнем на динаміку системи можна знехтувати. У цьому разі для дослідження цифрових систем можна застосувати математичний апарат дослідження лінійних імпульсних систем з амплітудно-імпульсною модуляцією: різницеві рівняння, дискретне Z-перетворення, частотні характеристики. Ось чому бажано добре засвоїти поняття передаточної функції імпульсної системи, методи оцінки її стійкості і якості, а також методи корекції та синтезу імпульсних систем з амплітудно-імпульсною модуляцією і використати ці знання для дослідження цифрових систем з ЦОМ.

Крім того, слід також пам’ятати імпульсну теорему (Котельникова – Шеннона), яка пов’язує частоту квантування  зі смугою пропускання частот неперервної частини системи. При досить великій частоті квантування імпульсна система еквівалентна неперервній. Кількісно умови еквівалентності визначаються такими нерівностями:

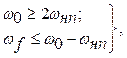                          (2.1)

 де

 – частота дискретності, Т₀ – період дискретності,

 – смуга пропускання неперервної частини системи;

 – найбільша частота вхідної дії.

При вирішенні задач цього розділу бажано використати матеріал за літературою: [1] – С.406-460; [2] – С. 336-363; [4] – С.284–298; [9] – С.304–372; [11] – С.214–304 та конспект лекцій.

2.1 Практичне заняття 3. Математичні моделі і стійкість ДСАК

2.1.1 Записати решітчасту функцію f[n] і всі її різниці, що відповідають неперервній функції f(t)=a∙t².

Розв’язання. Відповідно [1] – С. 414-416 решітчасту функцію, що відповідає неперервній функції f(t)=a∙t², визначають за формулою

                                                   (2.2)

або

             ,                                                               (2.3)

 де  – відносний час, а n=0,1,2,3,...,

 – період квантування.

Різниці неперервної функції f(t)=a∙t² відшукують по виразу

^,                                                                        (2.4)

звідки

^,                    (2.5)

,                                                          (2.6)

.                                        (2.7)

Тобто третя і подальші різниці дорівнюють нулю.

2.1.2 Записати решітчасту функцію f[nT₀], яка відповідає сумарному сигналу f(t), що складається з трьох складових, при наступних умовах: f₁(t)=2 при ; f₂(t)=0 при t<5; f₂(t)=0,5(t-5) при t; f₃(t)=0 при t<10;

f₃(t)=0,2(t-10)² при . Визначити значення функції при n=5, якщо період дискретності Т₀=2,5с.

Розв’язання.

                                       (2.8)

   ;

                             (2.9)

;

                       (2.10)

У відповідності з (2.82.10)

.      (2.11)

2.1.3 Структурна алгоритмічна схема дискретної цифрової системи наведена на рисунку 2.1.

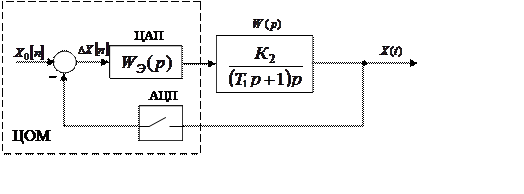
         Рисунок 2.1– Алгоритмічна схема цифрової системи.

Роботу ЦОМ забезпечує АЦП (квантователь) і ЦАП (екстраполятор нульового порядку) з передаточною функцією

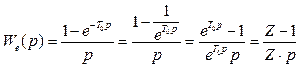,                           (2.12)

 де , К=10с^-1, Т₁=0,05с, Т₀=0,1с.

Треба визначити дискретну передаточну функцію

Розв’язання. Відповідно [1]– С.450– 453

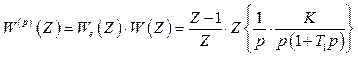.                           (2.13)

Подамо вираз у дужках у вигляді суми простих дробів і використаємо дані таблиці Zперетворювань ([1] – таблиця 10.1), тоді дістанемо

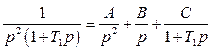,                                                (2.14)

 де                                      (2.15)

або ;               (2.16)

звідки А=1; В=-Т₁; С=Т₁².                                                       (2.17)

У відповідності з виразами (2.13÷2.17)

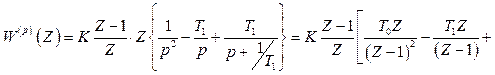
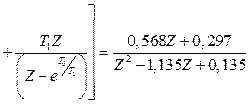.                                                    (2.18)

Ураховуючи (2.18), маємо

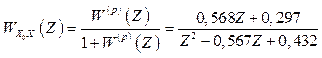.                      (2.19)

2.1.4 Оцінити стійкість замкненої дискретної системи, передаточна функція якої

.

Розв’язання. Характеристичне рівняння системи

.                                                   (2.20)

Знаходимо корні D(Z)

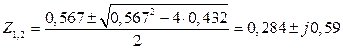.                              (2.21)

Модулі коренів Z_1,2

.                (2.22)

Замкнена цифрова система – стійка.

2.1.5 Оцінити за допомогою критерія Гурвіца стійкість замкненої імпульсної системи, характеристичне рівняння якої

.                                (2.23)

Розв’язання. Визначаємо стійкість системи за допомогою підстановки в (2.23)  відповідно [2]–С.355.

Після підстановки маємо

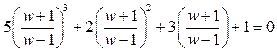                  (2.24)

або

.                                                      (2.25)

Система стійка, тому що виконуються умови критерія Гурвіца

2.1.6 Згідно з умовами задачі 2.1.3 побудувати ЛАЧХ і ЛФЧХ цифрової системи неперервна частина якої

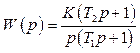 ,                                     (2.26)

 де К=10с^-1; Т₁=0,2с; Т₂=0,02с.

Період квантування Т₀=0,01с.

Побудувати також ЛАЧХ по виразу (2.26) неперервної частини цифрової системи і порівняти її з ЛАЧХ цифрової системи, яка відповідає передаточній функції

           ,                                (2.27)

 де – дискретна передаточна функція екстраполятора нульового порядку (2.12).

Розв’язання. Послідовність побудови ЛАЧХ і ЛФЧХ наступна:

.

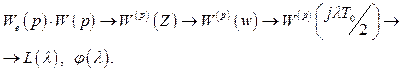Дискретна передаточна функція розімкненої цифрової системи (рисунок 2.1)

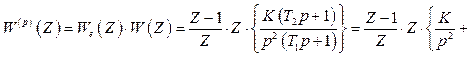
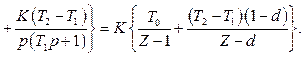                                      (2.28)

Виконаємо w-перетворення

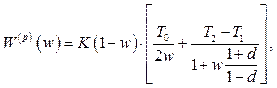                                (2.29)

        де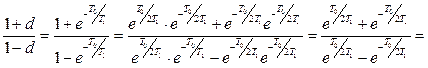

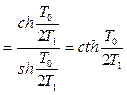.                                      (2.30)

За умовами задачі Т₁>0,5Т_0. Отже

.                                          (2.31)

Тоді 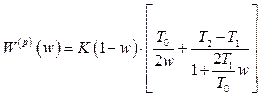.                        (2.32)

Підставимо у вираз (2.32)

                                               (2.33)

і перейдемо до частотної функції з псевдочастотою λ.

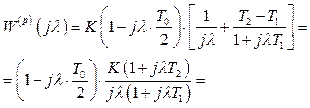
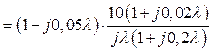                               (2.34)

Із виразу (2.34) отримуємо 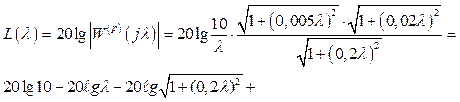 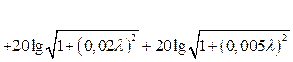                                          (2.35);

.           (2.36)

По (2.35) і (2.36) будуємо ЛАЧХ і ЛФЧХ цифрової системи. Вони наведені на рисунку 2.2.

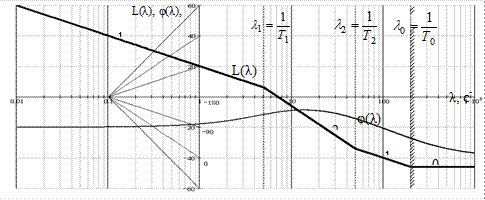
Рисунок 2.2– Логарифмічні частотні характеристики дискретної