Рассмотрим систему массового обслуживания с ожиданием, как наиболее общую систему обслуживания. Согласно уравнениям (11) и (6) математическая модель функционирования системы в стационарном режиме имеет вид:
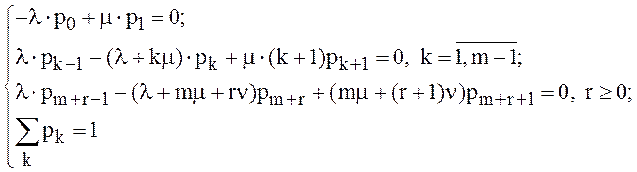 (12)
(12)
где
![]()
Обозначим через ![]() среднее
число требований (заявок), поступающих в систему обслуживания за среднее время
обслуживания одной заявки. Так как среднее число заявок, поступающих в систему
обслуживания в единицу времени равно
среднее
число требований (заявок), поступающих в систему обслуживания за среднее время
обслуживания одной заявки. Так как среднее число заявок, поступающих в систему
обслуживания в единицу времени равно![]() , а среднее время
обслуживания одной заявки равно
, а среднее время
обслуживания одной заявки равно![]() , то
, то
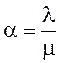 . (13)
. (13)
Величину ![]() называют приведённой
плотностью потока заявок.
называют приведённой
плотностью потока заявок.
Последовательно решив систему уравнений (12) (без последнего уравнения в ней), получим выражение вероятностей pk через p0:
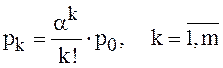 (14)
(14)
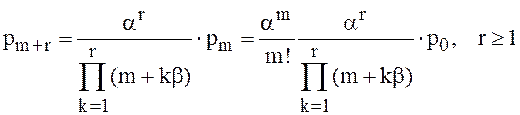 , (15)
, (15)
где
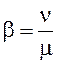 – приведенная плотность ухода заявок из
очереди.
– приведенная плотность ухода заявок из
очереди.
С использованием последнего равенства в системе (12) получим для р0 выражение:
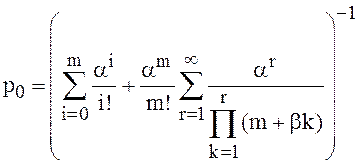 (16)
(16)
Среднюю длину очереди ![]() определяют как математическое ожидание числа
заявок в очереди. Из (15) находим
определяют как математическое ожидание числа
заявок в очереди. Из (15) находим
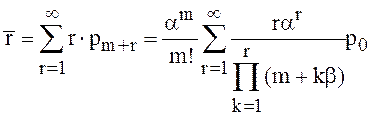 (17)
(17)
Формула (17) для вычисления ![]() достаточно
сложна. Для вычисления этой величины существует другой подход, следовательно,
другие формулы.
достаточно
сложна. Для вычисления этой величины существует другой подход, следовательно,
другие формулы.
Введем обозначение ![]() для
среднего числа занятых каналов обслуживания:
для
среднего числа занятых каналов обслуживания:
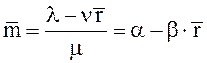 (18)
(18)
Формула
(18) получена в результате следующих рассуждений. Поскольку интенсивность ухода
из очереди равна![]() , то в единицу времени систему
покидает в среднем
, то в единицу времени систему
покидает в среднем ![]() заявок. Значит, из поступивших в
систему за единицу времени заявок будет обслужено
заявок. Значит, из поступивших в
систему за единицу времени заявок будет обслужено![]() .
.
Относительная пропускная способность системы
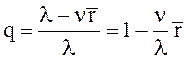 (19)
(19)
характеризует вероятность того, что заявка, поступившая в систему, будет обслужена. При отсутствии очереди, ( r=0), q=1.
Вернёмся к формуле (18). Воспользуемся тождеством 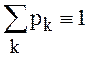 при n=
при n=![]() и тем фактом, что в состояниях Sm+r , r
и тем фактом, что в состояниях Sm+r , r![]() 0,
все каналы заняты и найдём
0,
все каналы заняты и найдём
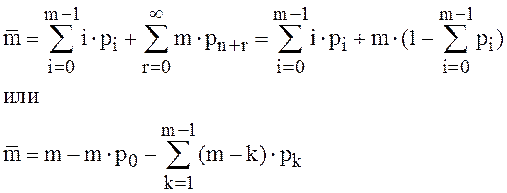 (20)
(20)
где вероятности рk находим по формулам (14), (16). Учитывая равенства (18) и (19) находим
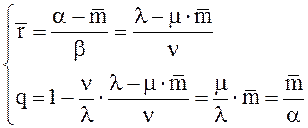 (21)
(21)
Так
называют СМО с ожиданием, в которой заявки не покидают очередь. Но тогда ![]() и
и![]() .
.
Из (16) находим:
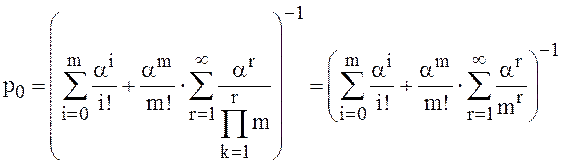 (22)
(22)
Если![]() , то ряд
, то ряд 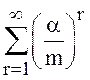 расходится, тогда p0=0 и согласно (14), (16) pk=0,
k=1,2,… Это означает, что стационарного режима работы
нет ( нарушается тождество
расходится, тогда p0=0 и согласно (14), (16) pk=0,
k=1,2,… Это означает, что стационарного режима работы
нет ( нарушается тождество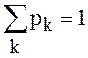 ), длина очереди
неограниченно возрастает, система не справляется с обслуживанием заявок.
), длина очереди
неограниченно возрастает, система не справляется с обслуживанием заявок.
Если![]() , то ряд сходится, его
сумму легко вычислить:
, то ряд сходится, его
сумму легко вычислить: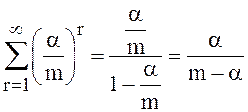 и для p0 получаем выражение
и для p0 получаем выражение
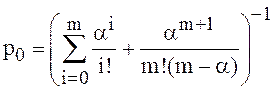 (23)
(23)
Средняя длина очереди в этом случае при ![]() =0 может быть найдена из (17):
=0 может быть найдена из (17):
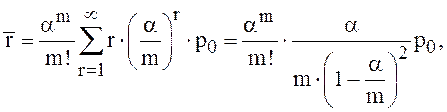 (24)
(24)
так как
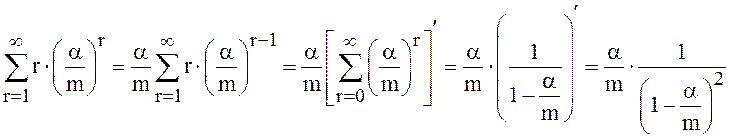
Пример 4. На железнодорожную сортировочную горку прибывают составы с интенсивностью 2 состава в час. Среднее время обработки состава составляет 0,4 часа. Если горка занята, прибывшие составы становятся в очередь в парке ожидания с тремя путями, каждый из путей предназначен для одного состава. Если заняты пути в парке ожидания, то состав ожидает очереди на внешней ветке. Найти: среднее число составов ожидающих обработки; среднее время пребывания в парке ожидания; среднее время пребывания состава на внешней ветке; среднее время пребывания на сортировочной горке, включая время ожидания и время обслуживания; вероятность того, что прибывший состав займёт место на внешней ветке.
В задаче ![]()
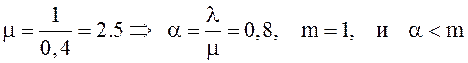 .
.
По формуле (22)
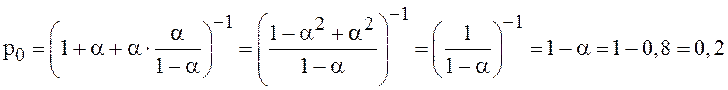 .
.
По
формуле (24) находим ![]()
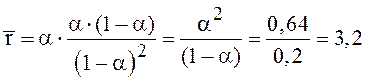 .
.
Событие {состав занимает место на внешней ветке} эквивалентно событию: {длина очереди больше 3}. Поэтому:
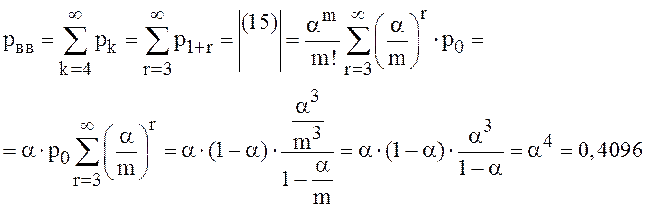 .
.
Среднее время ожидания на внешней ветке равно
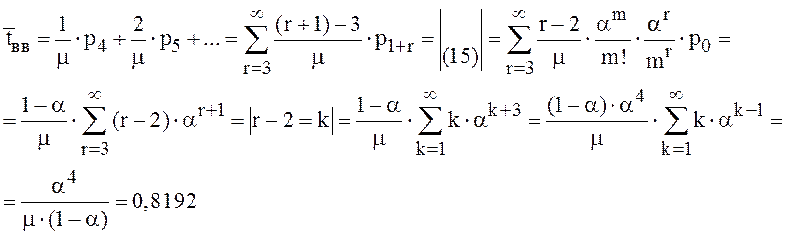
Среднее время ожидания в парке с тремя путями длиной в один состав равно
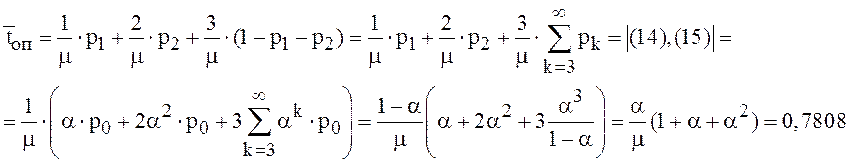 Среднее время ожидания в системе
Среднее время ожидания в системе![]() , а среднее время пребывания на сортировочной
горке равно
, а среднее время пребывания на сортировочной
горке равно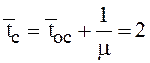 .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.