Стохастические модели состояния, страница 4

.                                           (12)

Тогда:

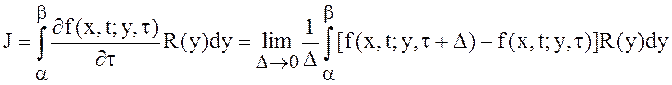    (13)

Согласно уравнению Чепмена – Колмогорова:

.

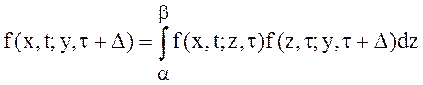Подставим это выражение в полученное равенство (13), получим:

         

==

.

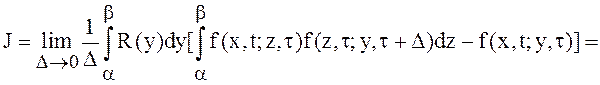
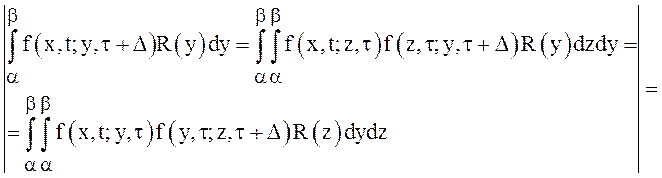
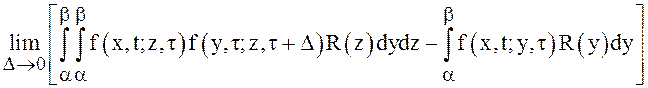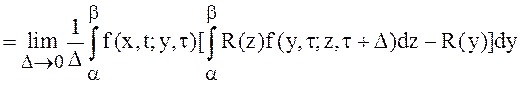Представим функцию  в виде:

,     .

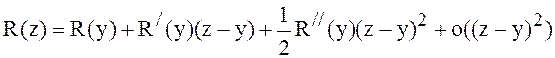Тогда:

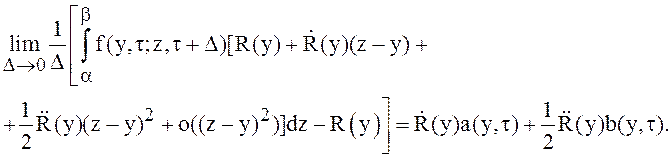
Для  получаем выражение:

.

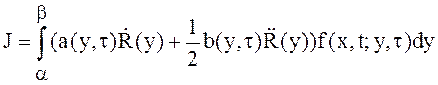Вычислим полученный интеграл по частям с учётом ограничений на  (12). Тогда  можно переписать в виде:

.

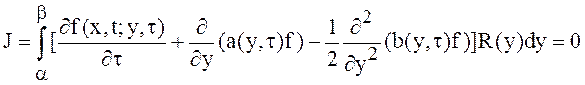Последнее равенство в силу произвольности функции  приводит к уравнению (11).

Уравнения Колмогорова (5) и (11) являются уравнениями в частных производных параболического типа. Чтобы решения были однозначны, нужны начальные и граничные условия.

Начальные условия устанавливаются обычно из смысла решаемой задачи. Для уравнения (11) естественно считать начальным значением переменной  настоящий момент времени. Но тогда

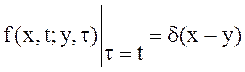                                                            (14)

по условию (1).

Начальные условия для обратного уравнения Колмогорова (5) вводят аналогично начальным условиям для прямого.

Граничные условия для уравнений Колмогорова фактически являются условиями изолированности области  изменения МП,. Условие изолированности области, если интерпретировать уравнения Колмогорова как уравнения массопереноса, означают, что соответствующие суммарные потоки обращаются на границе области в нуль. Следовательно, граничные условия для уравнения (8) могут быть заданы в виде:

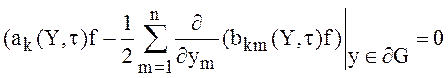,   ,                         (15)

а для уравнения (5) – в виде:

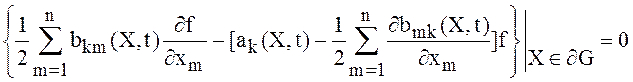,.   (16)

Если, то граничные условия (15), (16) упрощаются:

для обратного уравнения Колмогорова (5):

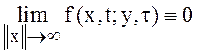,                                                              (17)

для прямого уравнения Колмогорова (11):

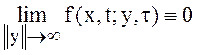.                                                                (18)

Заметим в заключение этого параграфа, что уравнение (5) может быть записано относительно плотности распределения сечения  - функции . Поскольку 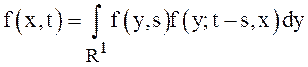, тогда (5) перепишется в  виде 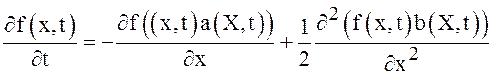,  которое решается с начальным условием , где  - плотность распределения .   

8.3. Стохастические модели состояния и уравнения Колмогорова

Пусть X(t), , – n-мерный случайный процесс, удовлетворяющий стохастической модели состояния в форме Ито:

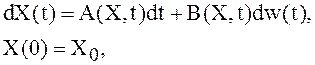                                     (20)

где W(t) – стандартный винеровский процесс.

Пусть при каждом фиксированном  функции  и  удовлетворяют условиям теоремы существования и единственности решения задачи Коши (20) и являются непрерывными  по  на промежутке,  - нормально распределенный вектор начальных условий.

Известно (7.2), что в этом случае стохастическая модель (20) задаёт марковский процесс X(t) и его условная плотность вероятности должна удовлетворять уравнениям Колмогорова (5) и (11), в которых функции  и  удовлетворяют равенствам (6) и (7).

Определим коэффициенты этих уравнений, для чего воспользуемся интегральным представлением стохастической модели состояния 

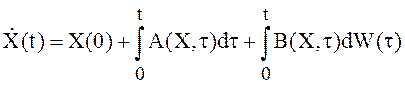                                   (21)

Имеем 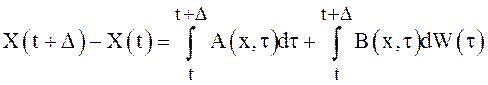. Второй интеграл в правой части  - интеграл Ито. Известно, что  математическое ожидание его равно нулю. Отсюда следует, что 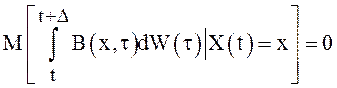. Далее, можно показать, что   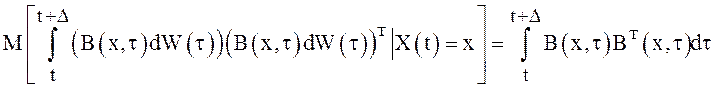  (22)

И с. величина  не зависит от приращений СП W(t) 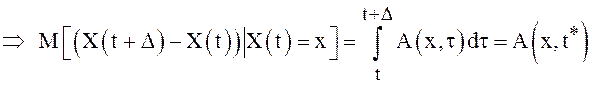, где  в силу непрерывности функции A(.,.) по параметру t. Подставим полученный результат в формулу (6) и при  получим            .

Далее, вычислим  по формуле (7) с учетом равенства (21), получим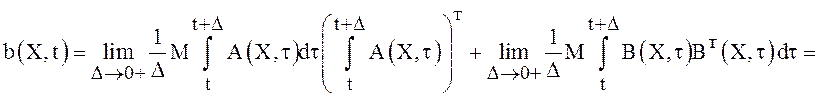

.

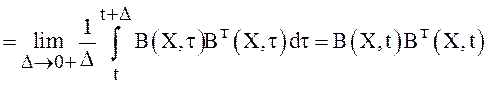Итак, получили  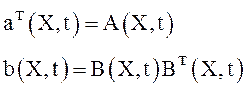                                              (23)

Итак, равенства (23)  позволяют реализовать переход от стохастической модели состояний (20) к уравнениям Колмогорова (5) и (11), которым удовлетворяет условная плотность вероятностей  марковского процесса X(t), , определяемого стохастической моделью состояний (20). А так как уравнения Колмогорова полностью определяются матричной функцией  и векторной функцией, то равенства (23) позволяют осуществить и обратный переход – от уравнений Колмогорова к стохастическому дифференциальному уравнению.