Стохастические модели состояния, страница 3

Первое условие обеспечивает непрерывность траекторий процесса с вероятностью 1. Функция  характеризует среднюю скорость смещения за малое время из состояния  и называется вектором сноса или дрейфа. Функция  характеризует отклонение процесса от его усредненного движения, определяемого вектором сноса, и называется матрицей диффузии.

Если для МП задана его переходная вероятность и соответствующие пределы в (1) -(3) определены, то тем самым определены его функции , . Однако центральным моментом теории диффузионных процессов является то, что задав достаточно регулярные функции ,  можно однозначно определить и переходную вероятность процесса.

Таким образом, локальное описание свойств траектории на языке коэффициента  сноса и диффузии позволяет определить и общие свойства процесса на всей временной оси. Метод построения переходных вероятностей предложен  А.Н. Колмогоровым и далее будет кратко изложен, не вдаваясь в технические детали, так как общая теория диффузионных процессов  весьма сложна.

Итак, пусть, , – n-мерный МП, , – фиксированные моменты времени. Для непрерывных  МП вместо переходных вероятностей обычно рассматривается условная переходная функция распределения.     Условную функцию распределения  называют марковской переходной функцией. Задание этой функции и вероятности начального состояния полностью определяют непрерывный марковский процесс (НМП).

В этой главе мы примем следующие обозначения: вместо  будем писать. Двумерную плотность вероятности, которую мы ранее обозначали как, будем теперь обозначать просто, одномерную –.

Поскольку процесс марковский, то все конечномерные распределения процесса определяются двумерным распределением, в частности:

     и     .

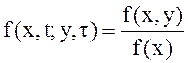8.1. Свойства марковских переходных функций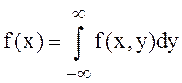

1., ,  является вероятностной мерой, то есть , ,.

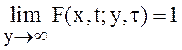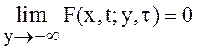2. Для всех, , , ,  удовлетворяет уравнению Чепмена – Колмогорова:

 

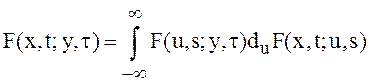
и, если условная функция распределения является абсолютно непрерывной, 

.

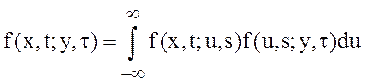Если  зависит только от –, то такой  непрерывный МП называется стационарным МП. Для него  и уравнение Чепмена – Колмогорова принимает вид:

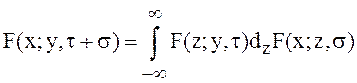
или

.

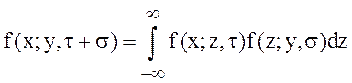Для условных плотностей вероятностей отметим свойства:

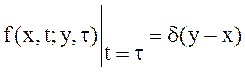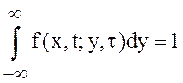
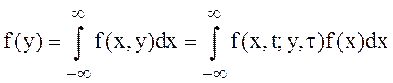, .                                            (4)    

8.2. Уравнения Колмогорова

Условная функция плотности вероятностей  n-мерного непрерывного марковского процесса X(t), , как функция параметров начального состояния  и, удовлетворяет уравнению:

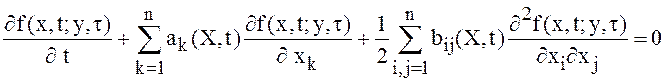.          (5)

Здесь   есть введенные равенствами (2) и (3) вектор  и функция . Равенства  (2) и (3) эквивалентны следующим:

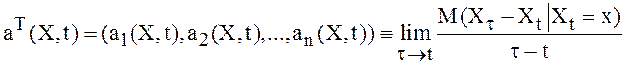             (6)

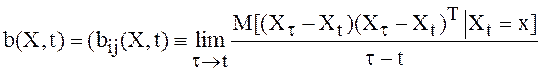                             (7)

Равенство (5) называют обратным уравнением Колмогорова. Его решение однозначно определяет МП. 

Выведем уравнение (5). Пусть, , – скалярный МП и  – его условная плотность вероятностей. В уравнении Чепмена – Колмогорова при  полагаем, где  и запишем его в виде:

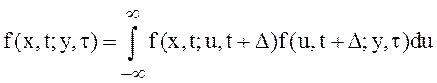.                         (8)

Функцию  разложим по формуле Тейлора в окрестности точки:

          ,.

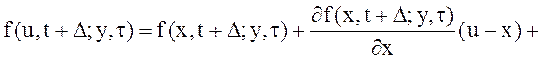
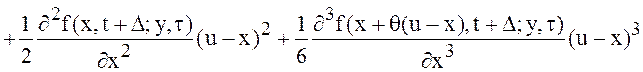Выражение (8) принимает вид:

         

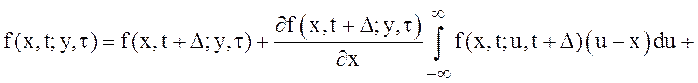
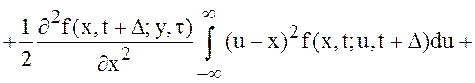
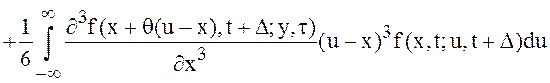.                           (9)

Интеграл в первом слагаемом в правой части равен 1 по свойствам (4). Перенесём  в левую часть, поделим обе части равенства на  и перейдём к пределу при. В результате получим уравнение (5), в котором функции  и  заданы соотношениями (6), (7). Но при этом потребовали, чтобы:

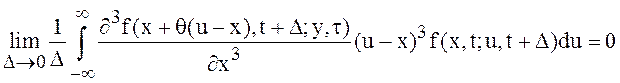.             (10)

Требование (10) означает, что вероятность больших отклонений  с изменением  снижается, причём все моменты с. в., начиная с третьего, имеют порядок малости,.

Рассмотрим теперь функцию  как функцию параметров  и. В этом случае  удовлетворяет уравнению:

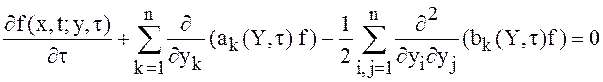.                (11)

Это уравнение носит название прямого уравнения Колмогорова или уравнения Фоккера – Планка, поскольку оно встречалось в работе этих учёных ещё до того, как его обосновал А.Н.Колмогоров.

Вывод уравнения (11) осуществляется более искусственным способом.

Пусть,  – границы изменения скалярного МП X(t), , с условной плотностью вероятности, а  – любая дважды непрерывно дифференцируемая неслучайная функция, удовлетворяющая условиям: