Уравнения (6), (7) называются уравнениями метода моментов.
Приведем обоснование этого метода. Воспользуемся
формулой (4), дающей явный вид решения уравнения (3). Вычислим математическое
ожидание и дисперсионную матрицу процесса X(t). ![]() ,
поскольку известно, что математическое ожидание стохастического интеграла от
неслучайной функции равно нулю. Дифференцирование полученного равенства по t
дает уравнение (3). Далее, вычтем из равенства (4) полученное выражение для
,
поскольку известно, что математическое ожидание стохастического интеграла от
неслучайной функции равно нулю. Дифференцирование полученного равенства по t
дает уравнение (3). Далее, вычтем из равенства (4) полученное выражение для ![]() , получим
, получим
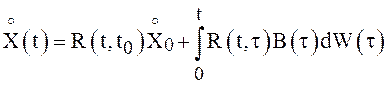 ,
(8)
,
(8)
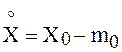 . Обозначим стохастический интеграл от
неслучайной функции в правой
части равенства (8) через
. Обозначим стохастический интеграл от
неслучайной функции в правой
части равенства (8) через 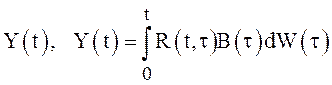 . По свойству
стохастических интегралов от неслучайных функций имеем
. По свойству
стохастических интегралов от неслучайных функций имеем
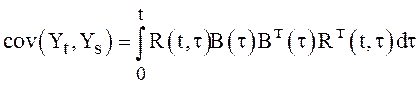 (9)
(9)
Учитывая независимость ![]() получаем
получаем
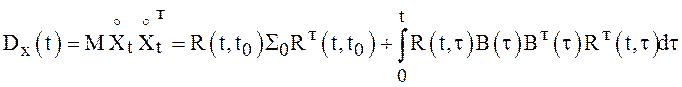 . Продифференцируем полученное выражение
по t:
. Продифференцируем полученное выражение
по t: 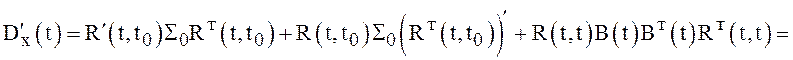
![]()
![]() =
= ![]() .
.
Справедливо утверждение [7]: если в модели (3)
дополнительно![]() - с. величина, имеющая нормальное
распределение с параметрами m0 и S0 и не
зависит от СП W(t), t >0, то решение задачи Коши (3) является нормальным
Марковским процессом. При этом
- с. величина, имеющая нормальное
распределение с параметрами m0 и S0 и не
зависит от СП W(t), t >0, то решение задачи Коши (3) является нормальным
Марковским процессом. При этом
![]() (10)
(10)
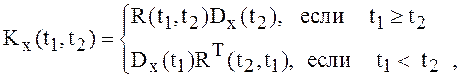 (11)
(11)
Пример 1. Пусть в задаче (3) X(t), tÎT, - двумерный СП и A(t)=A=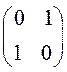 , B(t)=B=
, B(t)=B=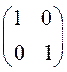 , X0=
, X0=![]() . Найдем вероятностные
характеристики СП X(t), tÎT.
. Найдем вероятностные
характеристики СП X(t), tÎT.
Прежде всего, матрицы A и 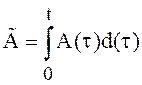 перестановочны:
перестановочны: 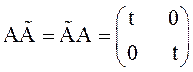 ,
,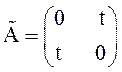 . Тогда резольвенту R(t,s)
для системы (6) ищем в виде R(t,s)=R(t-s)=R(t)=
. Тогда резольвенту R(t,s)
для системы (6) ищем в виде R(t,s)=R(t-s)=R(t)= ![]()
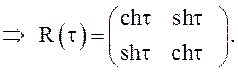 Тогда
решение (6) можно записать в виде равенства (10), то есть
Тогда
решение (6) можно записать в виде равенства (10), то есть
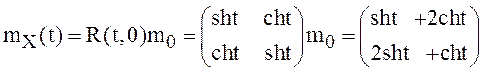 .
.
Рассмотрим теперь уравнение (7).
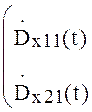
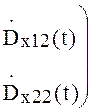 =
= 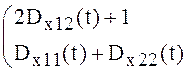
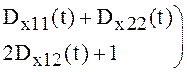 ,
, ![]() . Решением системы служит матрица
. Решением системы служит матрица 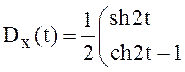
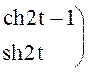 .
.
Для
![]() может быть получено выражение согласно
формуле (11).
может быть получено выражение согласно
формуле (11).
Из утверждений, сформулированных выше, можно сделать следующие выводы:
1.Так как СП![]() ,
, ![]() , описываемый равенством (3), является
нормальным, то кроме математического ожидания процесса
, описываемый равенством (3), является
нормальным, то кроме математического ожидания процесса ![]() и
его ковариационной функции
и
его ковариационной функции ![]() можно записать
одномерное распределение СП с помощью плотности вероятностей:
можно записать
одномерное распределение СП с помощью плотности вероятностей: 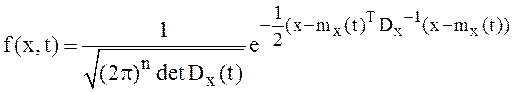 .
.
2.Поскольку СП ![]() марковский,
то его N-мерная плотность вероятностей
марковский,
то его N-мерная плотность вероятностей ![]() может
быть записана в виде:
может
быть записана в виде: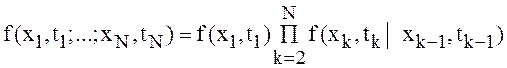 , где плотность вероятностей:
, где плотность вероятностей:
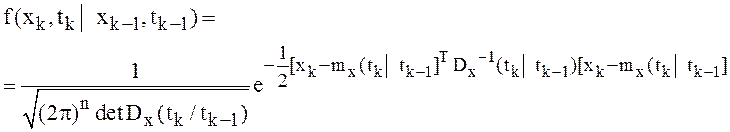 (12)
(12)
При этом ![]() и
и ![]() являются
решениями следующих задач Коши:
являются
решениями следующих задач Коши:
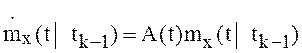 ,
, ![]() ,
,
![]() ,
(13)
,
(13)
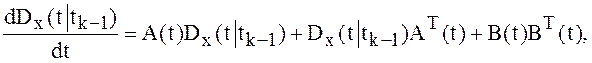 (14)
(14)
![]()
3.
Если в стохастической задаче Коши (3)![]() ,
, ![]() ,
, ![]() , причём
действительные части всех собственных чисел матрицы А отрицательные, то при
, причём
действительные части всех собственных чисел матрицы А отрицательные, то при ![]() решение
решение![]() ,
, ![]() , этой задачи можно считать стационарным (в
широком смысле) нормальным марковским СП.
, этой задачи можно считать стационарным (в
широком смысле) нормальным марковским СП.
Пример 2. Пусть скалярный СП![]() ,
, ![]() ,
является решением стохастической задачи Коши:
,
является решением стохастической задачи Коши:
![]()
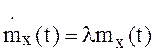 ,
,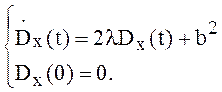 . Решение
имеет вид:
. Решение
имеет вид: 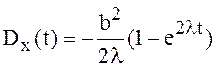 ,
, ![]() ,
, ![]() .
.
Выражение
для ![]() при
при ![]() принимает
вид:
принимает
вид:
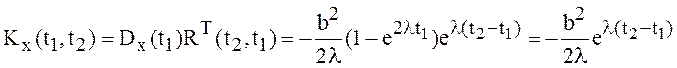 при
при ![]() и
и ![]() .
.
Следовательно, ответ на вопрос задачи утвердительный.
Найдём ![]() по известной формуле (9) гл. IV:
по известной формуле (9) гл. IV: 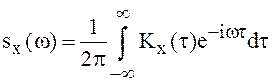 . Отметим, что при
. Отметим, что при
![]()
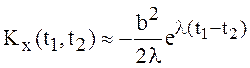 ,следовательно,
,следовательно, 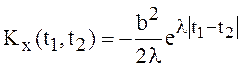
![]()
![]() . Кроме того, пусть
. Кроме того, пусть ![]() . Тогда имеем
. Тогда имеем
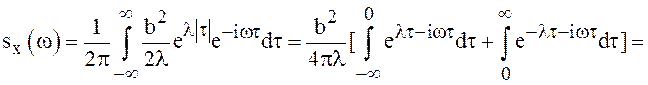
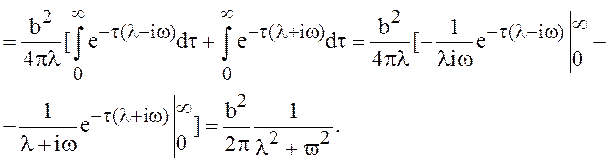
Это такие МП, в которых пространство состояний X - непрерывное множество, и время изменяется также непрерывно. Такие процессы являются естественной моделью для описания эволюции динамических систем, подверженных случайным воздействиям. Наиболее изученными в настоящее время являются процессы диффузионного типа или просто диффузионные процессы.
Определение 1. Случайный
однородный МП X(t) называется процессом диффузионного типа, если его переходная
вероятность (см. 2.4) ![]() удовлетворяет следующим
условиям:
удовлетворяет следующим
условиям:
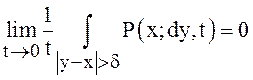 (1)
(1)
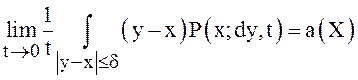 (2)
(2)
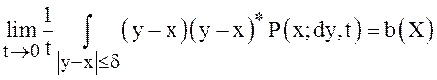 (3)
(3)
для
любых ![]()
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.