Стохастические модели состояния, страница 10

Это системы, в которых вновь поступающая заявка покидает систему, если все m каналов обслуживания заняты. Система имеет конечное число состояний S_k,;, значит и. При малом числе каналов можно воспользоваться основными формулами (14),(16),(20) при условии r=0. При этом сама система уравнений Колмогорова (1 принимает вид:

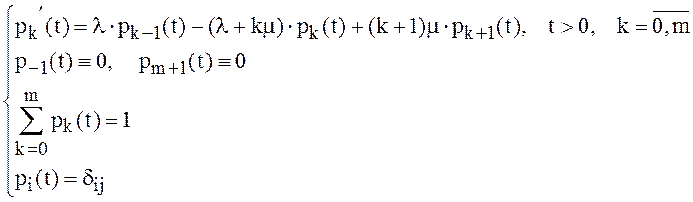  (25)

Из  (14), (16)

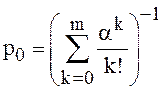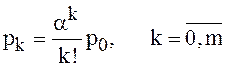,   .                                              (26)   

Если ввести обозначения, которые применял датский инженер А.К.Эрланг при исследовании систем обслуживания с отказами применительно к телефонной связи:

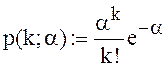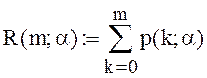,,                                            (27)

то приходим к формулам:         

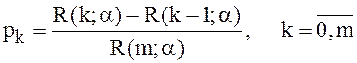,                                                (28)

которые в литературе по ТМО носят название формул Эрланга.

Формулами Эрланга удобнее пользоваться при больших значениях k, так как в этом случае

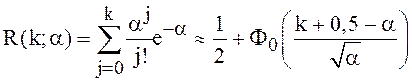, где

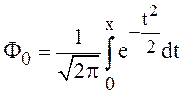– функция Лапласа.                                                      (29)

Вероятность отказа в таких системах равна вероятности того, что все каналы заняты,  

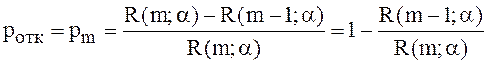                                     (30)

Вероятность того, что заявка, поступившая в систему, будет обслужена, есть не что иное, как относительная пропускная способность системы q,

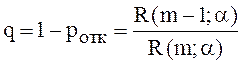                                                                               (31)

Среднее число занятых в системе каналов равно

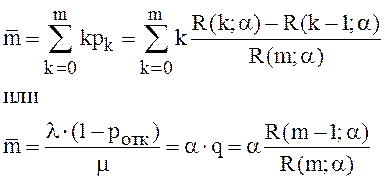                                    (32)     и – среднее число заявок, обслуженных в единицу времени – абсолютная производительность системы, а– среднее число заявок, обслуживаемое одним каналом.

Пример 5. АТС обеспечивает не более 120 переговоров одновременно. Средняя продолжительность переговоров 60 секунд, вызовы в среднем поступают через 0,5 секунд. Найти: среднее число занятых каналов, относительную пропускную способность q, среднее время пребывания заявки в системе с учётом, что разговор может и не состояться.

В задаче m=120, 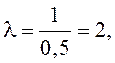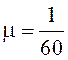.   Из этих данных получаем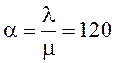. ( Если бы система была системой с ожиданием , то она не справлялась бы с работой).

Среднее число занятых каналов будем искать по второй формуле(32). Для этого нужны величины R(120;120) и R(119;120). С помощью формулы (29) по таблицам находим

.

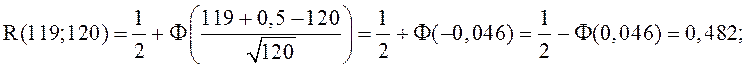
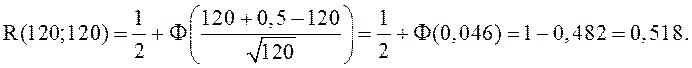Тогда

.

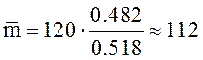Далее, согласно формуле (31),

.

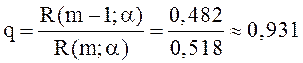Интенсивность входного потока–число заявок, поступающее в среднем в систему за единицу времени. Тогда– среднее время пребывания заявки в системе, то есть. В примере 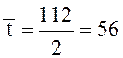(сек).

9.7.3. Системы обслуживания с ограниченной

длиной очереди

В системе из каналов и длиной очереди  интенсивность  ухода заявок из системы зависит от её состояния S_k,

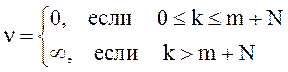                                      (33)          

Число состояний S_k системы конечно,.

Математическая модель системы в рамках предположений о входном потоке и времени обслуживания, сделанных в пункте 9.3, имеет вид:

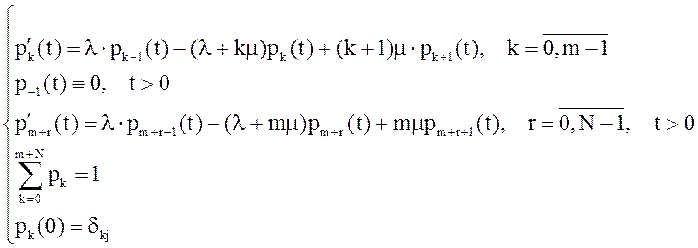             (34)

где и j–некоторый фиксированный элемент множества {0,1,2,…,m+N}.

Поскольку нас будут интересовать вероятности, , полагают что (см. соотношения (33)). Но тогда и  и использование формул (14),(16) даёт следующие результаты:

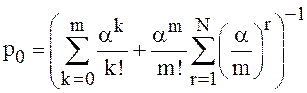                                              (35)

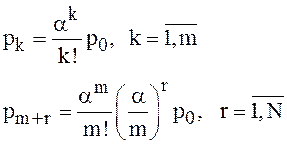                                                  (36)

Вероятность заявке получить отказ, как и в системах массового обслуживания с отказами (раздел 9.7.2) равна:

                                                                             (37)

Относительная пропускная способность системы

                                                            (38)

9.7.4. Замкнутые системы обслуживания

Это частный случай систем обслуживания с ограниченной длиной очереди. Рассмотрим этот тип СМО на конкретном примере.

Пример 6. Два рабочих обслуживают 6 однотипных станков. Остановка работающего станка происходит в среднем каждые полчаса, процесс наладки в среднем занимает 10 минут. Найти: среднюю занятость рабочих, среднее количество неисправных станков, абсолютную пропускную способность рабочей бригады.

В примере 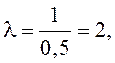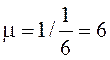,  N=6. Возможны состояния: S₀ – станки работают, рабочие свободны; S₁ –один станок остановился, занят один рабочий, второй свободен; S₂ –два станка остановились, рабочие заняты; S_2+r – два станка остановились, рабочие заняты, r станков стоят в очереди на обслуживание, .