Стохастические модели состояния, страница 8

        Пример 2. Одноканальная система обслуживания представляет собой телефонную линию. Заявка-вызов, поступившая в систему, если канал занят, получает отказ. Интенсивность потока заявок  (число вызовов в минуту). Средняя продолжительность разговора 1,5 мин. Считая входной поток заявок простейшим, а время обслуживания распределённым по экспоненциальному закону с параметром, определим в установившемся (стационарном) режиме а); б); в) вероятность отказа.

Имеем ,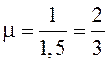.   Тогда по формуле (5): 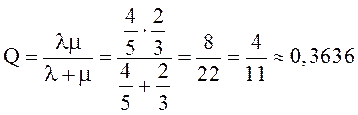,     а по формуле (6): 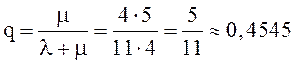--это вероятность того, что заявка будет обслужена (не получит отказ). Тогда:      .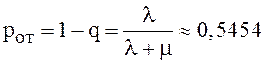

Интересно отметить, что  – номинальная пропускная способность канала связи, почти вдвое больше его пропускной способности. Это объясняется случайным характером потока заявок и времени их обслуживания.

Выведем теперь некоторые соотношения и введём понятия, которыми мы пользовались при решении задач 1 и .

9.5. Системы массового обслуживания с ожиданием

Будем пользоваться обозначениями п. 9.3. Полагаем, что в момент времени  система находится в состоянии,. Вероятность того, что за временной интервал  (бесконечно малой длительности) она из состояния  перейдёт в состояние, зависит лишь от потока заявок, следовательно:

,. Но тогда:

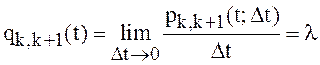.                                      (7)

Переход из состояния  в состояние  зависит лишь от освобождения каналов обслуживания. Поскольку

,Следовательно,   

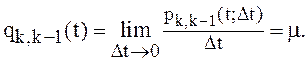                                          (8)

Эти рассуждения относятся к системе с одним каналом обслуживания.

Если же каналов обслуживания m и из них в момент  занято i каналов, то в силу независимости их функционирования  интенсивность обслуживания увеличивается в i раз, то есть

                                                                             (9)

При возникновении очереди  интенсивность обслуживания  становится постоянной, равной mμ , так как на освободившийся канал сразу же поступает очередная заявка.

Переход из состояния в состояние  может быть вызван не только тем, что обслуженная заявка покидает систему, но и тем, что заявка из очереди покидает систему, если время ожидания в очереди  ограниченное. Закон распределения времени ожидания  определяется интенсивностью ν ухода из очереди при наличии в ней одной заявки. В силу независимости поступления заявок, интенсивность, с которой заявки отказываются от обслуживания, равна rν.

Следовательно, плотность вероятности перехода системы из состояния  в состояние  равна сумме интенсивностей освобождения каналов обслуживания и отказа от обслуживания:

                                                          (10)

Граф состояний системы с ожиданием выглядит следующим образом:

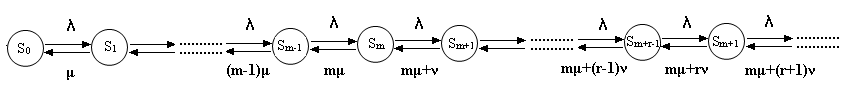
Воспользуемся этим графом и правилом построения системы уравнений Колмогорова:

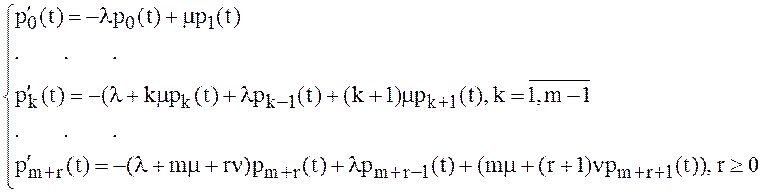(11)       Если в начальный момент времени система находится в одном из своих состояний , то начальные условия  для нее имеют вид: . 

   Пример 3. Запишем уравнения Колмогорова для одноканальной системы обслуживания с ожиданием, количество мест в очереди ограничено, равно N.

Система имеет возможные состояния:

-S₀ – канал свободен;

-S₁ – канал занят, но очереди нет;

-S_1+j – канал занят, и в очереди находится j заявок, 1 j N.

Единственной причиной отказа служит отсутствие мест в очереди, следовательно,  интенсивность ухода из очереди.

Нарисуем размеченный граф состояний системы:

Он облегчает составление уравнений Колмогорова:

                  

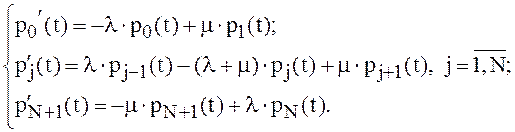
Задав начальные условия, получаем единственное решение системы уравнений.

9.6. Стационарный режим функционирования

 (общие соотношения)

Стационарный режим работы, если он существует, является предельным () случаем функционирования системы, когда в ней заканчиваются все переходные процессы. В стационарном режиме работы система также меняет свои состояния случайным образом, но вероятности состояний (вектор p(t)) уже не зависят от времени. Каждая компонента вектора p(t)p=(p₁, p₂, …, p_n) характеризует относительное время пребывания системы в данном состоянии.