Стохастические модели состояния

VII.Стохастические модели состояния

В  3.14 мы ввели в рассмотрение стохастическое дифференциальное уравнение (30), (31). В этом разделе мы  рассмотрим один из практических способов получения уравнений такого вида и рассмотрим общий вид решений для линейных уравнений.

7.1. Общие определения.

Рассмотрим математическую модель, описывающую эволюцию изучаемого объекта на отрезке времени T=[0,T],  следующим образом:

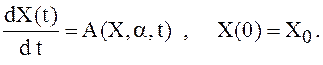                           (1)

Здесь X(t) – n-мерный вектор, описывающий состояние системы, a - вектор параметров, не зависящих от времени, А – n-мерная функция m+n+1 переменного, удовлетворяющая условиям существования и единственности решения задач Коши (1), –  начальное состояние.

Это детерминированная (неслучайная) модель состояния является достаточно общей и может описывать широкий класс детерминированных систем.

Теперь в правую часть ОДУ добавим n-мерный СП h(t), tÎT, который назовем процессом случайных возмущений. В общем случае считается, что h зависит от X(t), a, t, то есть  h = h( Х, a ,t ), и эту зависимость мы представим в виде h(Х,a,t) = B(Х,a,t)x(t), где  B(Х,a,t) – n-мерная неслучайная функция n+m+1 переменного, а x(t) – некоторый СП.       Новая, стохастическая модель состояния запишется в виде

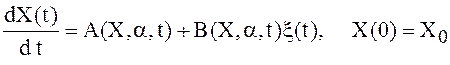                           (2) 

Анализ этой модели без конкретизации свойств СП x(t), tÎT, невозможен. Каким условиям должен удовлетворять СП x(t), tÎT ?        

1. Не теряя общности дальнейших рассуждений можно считать, что. 

2. Чтобы сохранить основное свойство модели (1), состоящее в том, что скорость изменения состояния определяется   текущим состоянием и не зависит от его предыстории, следует потребовать независимости любых двух сечений СП  x(t) - с.величин    и, то есть.

3. Для  сохранения  непрерывности  производной   следует потребовать с.к. непрерывности СП  , а это равносильно ограниченности  то есть.

Можно показать [7], что СП x(t), tÎT, удовлетворяющий требованиям 1-3, может иметь только нулевую дисперсию. Это означает, что в смысле среднего квадратичного, то есть   Более того, не существует  СП x(t), tÎT, с независимыми сечениями и ограниченной дисперсией. Далее, если X(t) – решение задачи (1), а - решение задачи (2), то=X(t) в среднем квадратичном, и значит - неслучайная функция. Это значит, что стохастическая модель (2) не дает никакой новой информации по сравнению с исходной моделью (1).

Этот результат является следствием слишком жестких требований, налагаемых на СП x(t), tÎT. Первое требование несущественно, отказ от второго требования вызовет не только вычислительные, но и теоретические трудности. Потому отказываются от требования 3. Но СП с независимыми сечениями и бесконечной дисперсией – это белый шум  ковариационная функция которого имеет вид где некоторая матрица. Для стационарных СП  ковариационная матрица  поcтоянна, тогда спектральная плотность СП 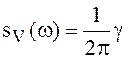, то есть  также не зависит от частоты. Матрицу   называют матрицей спектральных плотностей или интенсивностей или просто интенсивностью белого шума.

7.2.  Линейные стохастические модели состояний

Исследование нелинейных стохастических моделей (нелинейных по X(t)) (2) связано со значительными трудностями принципиального характера. Оно значительно упрощается, если рассматривать линейные стохастические модели

                        (3)

Здесь A и B – известные матричные функции параметра t и α, но для простоты записи вектор параметров α  писать не будем. W(t) – стандартный винеровский процесс, выходящий из 0; - с. величина, характеризующая начальное состояние. В дальнейшем изложении матрицы A и B будем считать непрерывными по t. Если эти матрицы постоянны в модели (3), то система (3) называется однородной. Модель (3) еще называют стохастической моделью состояния в форме Ито (см..

Для любого  стохастическая задача (3) переходит в задачу Коши для ОДУ, причем выполнены условия существования и единственности решения этой задачи, следовательно, при любом    задача Коши (3)  однозначно определяет соответствующую реализацию СП    Таким образом, стохастическая задача Коши (3) определяет всю совокупность возможных реализаций рассматриваемого СП X(t), tÎT.

Решение системы уравнений  (3) имеет вид, аналогичный указанному в 3.5.1,   

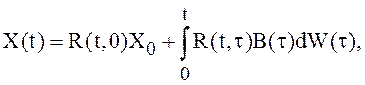                                       (4) где R(t,)= - нормированная фундаментальная матрица решений или резольвента. Резольвента R(t,)  удовлетворяет условиям :

                                      (5)

и функция  - есть решение системы .

Для линейных стохастических дифференциальных уравнений  известен метод вычисления моментных характеристик 1-го и  2-го порядков решения (4), называемый методом моментов.

Теорема 1. Пусть СП X(t) удовлетворяет линейной системе стохастических дифференциальных уравнений (3), в момент времени t >0 имеет вероятностные характеристики  и ковариационную матрицу , начальное значение  не зависит от процесса , то функции  являются решениями следующих ОДУ

                                              (6)

        (7)