Стохастические модели состояния, страница 6

11. Как связаны между собой параметры уравнений Колмогорова и соответствующей стохастической модели состояния?

12. Пусть X(t) является решением стохастической задачи Коши 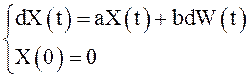, где a, b – неслучайные параметры. Можно ли этот процесс считать стационарным в широком смысле по прошествии некоторого времени? Если да, то чему равна его спектральная плотность?

IX. Элементы теории массового обслуживания

9.1. Основные понятия

На практике часто приходится сталкиваться с процессами, имеющими следующую общую структуру:

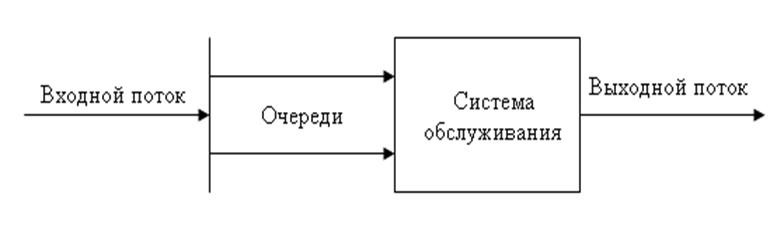
Промежутки времени, через которые поступают объекты, и время их обслуживания, как правило, имеют случайный характер. Поэтому в системе обслуживания могут возникнуть очереди.

Процессы, объединённые общей структурой, изображённой на рисунке, называются процессами массового обслуживания (ПМО).

Они типичны для связи, транспорта, культурно-бытовых предприятий, производственных процессов и т. д.

Вне зависимости от конкретной природы и характера объектов, поступающих в систему обслуживания (СО) их называют заявками или требованиями. Входной поток заявок рассматривают как последовательность случайных событий. Закон распределения входного потока в значительной степени обуславливает характер процесса массового обслуживания.

Дисциплина очереди может быть самая различная: заявки могут выполняться по мере поступления, с приоритетом, в случайном порядке и т. д. Очереди могут ограничиваться по длине, по времени ожидания. В конечном счёте основной характеристикой очереди является время ожидания обслуживания.

Система обслуживания состоит из определённого числа обслуживающих единиц, называемых каналами обслуживания, и может также иметь различную организацию: с последовательными, параллельными, комбинированными каналами и т. д. По занятости каналов СО делятся на системы обслуживания с отказом (если канал занят, заявка получает отказ), СО с очередями или СО с ожиданием.

Изучение процессов массового обслуживания  составляет предмет теории массового обслуживания.

9.2. Простейший поток

Входной поток называется простейшим, если он представляет собой пуассоновский процесс. Все свойства простейшего потока – это свойства пуассоновского процесса.

На практике в «чистом» виде простейшие потоки встречаются, видимо, достаточно редко, с нарушением требований, предъявляемых к ним. Однако сумма бесконечного числа ординарных стационарных потоков с практически любым последействием является простейшим потоком.

9.3. Время ожидания и время обслуживания

Мы будем рассматривать СО, в которых время обслуживания заявки есть величина, распределённая по экспоненциальному закону с параметром, то есть:     . Многие реальные системы вполне удовлетворительно описываются такими моделями.

Известно, что среднее время обслуживания заявки равно. Величину  называют интенсивностью обслуживания. Функция распределения: ,определяет вероятность того, что к моменту  обслуживание будет завершено.

Время ожидания также случайная величина, распределённая по экспоненциальному закону с параметром: . Среднее время ожидания равно, вероятность того, что в момент времени  начнётся обслуживание заявки, определяет функция распределения: .

9.4. Некоторые типы марковских моделей

систем массового обслуживания

Отметим прежде всего, что процессы массового обслуживания – это случайные процессы с дискретными состояниями. Переход из одного состояния в другое происходит скачком в момент времени, когда реализуется случайное событие: поступление новой заявки, окончание обслуживания заявки и т. д., вызывающее переход системы в новое состояние. Процессы массового обслуживания с простейшим входным потоком и экспоненциальным временем обслуживания – марковские СП с дискретными состояниями. Это значит, что развитие таких процессов определяется текущим состоянием и не зависит от его предыстории.