Введём обозначения:
пусть ![]() – возможное состояние системы,
– возможное состояние системы, ![]() , где
, где ![]() – число
каналов системы. Оно означает, что в системе занято ровно
– число
каналов системы. Оно означает, что в системе занято ровно ![]() каналов обслуживания;
каналов обслуживания; ![]() – состояние означает, что все
– состояние означает, что все ![]() каналов обслуживания заняты и в очереди
стоят
каналов обслуживания заняты и в очереди
стоят ![]() заявок,
заявок,![]() . Если
на длину очереди не накладывают ограничений, то
. Если
на длину очереди не накладывают ограничений, то ![]() может
быть сколь угодно большим и система имеет счётное множество состояний. Системы
с ограничениями на длину очереди и системы с отказами (заявка покидает систему,
если в момент её поступления все каналы обслуживания заняты) имеют лишь
конечное число состояний. В любой момент времени, таким образом, система
обслуживания с
может
быть сколь угодно большим и система имеет счётное множество состояний. Системы
с ограничениями на длину очереди и системы с отказами (заявка покидает систему,
если в момент её поступления все каналы обслуживания заняты) имеют лишь
конечное число состояний. В любой момент времени, таким образом, система
обслуживания с ![]() идентичными каналами находится в
одном из своих состояний
идентичными каналами находится в
одном из своих состояний![]() , при этом:
, при этом:
-если ![]() , то занято
, то занято ![]() каналов
и очереди нет;
каналов
и очереди нет;
-если ![]() , то заняты все каналы и в очереди
находятся
, то заняты все каналы и в очереди
находятся ![]() заявок,
заявок, ![]() ;
;
-если ![]() , то система обслуживания с отказами;
, то система обслуживания с отказами;
-если ![]() , то систем с ограниченной длиной очереди;
, то систем с ограниченной длиной очереди;
-если ![]() , то систем с ожиданием (без ограничения на
длину очереди).
, то систем с ожиданием (без ограничения на
длину очереди).
Обозначим за ![]() событие, состоящее в том, что в момент
времени
событие, состоящее в том, что в момент
времени ![]() система находится в состоянии
система находится в состоянии![]() ,
, ![]() ,
,![]() . Очевидно, что события
. Очевидно, что события ![]() образуют полную группу событий,
следовательно:
образуют полную группу событий,
следовательно:
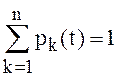 . (1)
. (1)
Одна из задач ТМО сводится к
нахождению вектора ![]() как функции времени.
как функции времени.
Из приведённых выше
рассуждений и определения ДМП следует, что процесс обслуживания с простейшим
входным потоком и экспоненциальным временем обслуживания является процессом
гибели – размножения. Для размеченного графа такого процесса введём
терминологию, принятую в ТМО. Элемент графа, соответствующий возможному
состоянию системы ![]() ,
, ![]() , называют
k-ой вершиной графа; стрелки с означенными
вероятностями перехода из одного состояния в другое – нагруженными дугами;
переходные вероятности – весами. Пользуются следующим правилом при составлении
уравнений Колмогорова: производная от вероятности пребывания системы в момент
времени
, называют
k-ой вершиной графа; стрелки с означенными
вероятностями перехода из одного состояния в другое – нагруженными дугами;
переходные вероятности – весами. Пользуются следующим правилом при составлении
уравнений Колмогорова: производная от вероятности пребывания системы в момент
времени ![]() в состоянии
в состоянии![]() ,
, ![]() , равна сумме произведений весов дуг,
инцидентных данной вершине графа, на вероятность состояний, от которых они
направлены. При этом вес дуги берётся со знаком «+», если дуга направлена к k-ой вершине графа и со знаком «–» в противном случае.
, равна сумме произведений весов дуг,
инцидентных данной вершине графа, на вероятность состояний, от которых они
направлены. При этом вес дуги берётся со знаком «+», если дуга направлена к k-ой вершине графа и со знаком «–» в противном случае.
Пример 1.
Рассмотрим простейшую задачу ТМО – задачу функционирования одноканальной
системы обслуживания с отказами с простейшим входным потоком с параметром ![]() . Параметр экспоненциального времени обслуживания –
. Параметр экспоненциального времени обслуживания –![]() .
.
Система имеет только
два состояния: ![]() – канал свободен,
– канал свободен, ![]() – канал занят. Размеченный граф состояний
имеет вид:
– канал занят. Размеченный граф состояний
имеет вид:
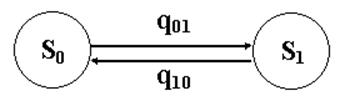
Далее
мы докажем, что ![]() ,
,![]() .
Система уравнений Колмогорова (математическая модель процесса) имеет вид (при
условии, что в начальный момент система находилась в состоянии
.
Система уравнений Колмогорова (математическая модель процесса) имеет вид (при
условии, что в начальный момент система находилась в состоянии![]() ):
):
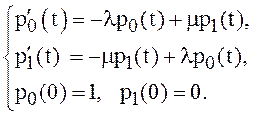 (2)
(2)
С
учётом равенства (1): ![]() ,
, ![]() , модель
процесса можно упростить:
, модель
процесса можно упростить:
![]() . (3)
. (3)
Решением
задачи Коши (3) служит вектор ![]() , определяемый
соотношениями:
, определяемый
соотношениями:
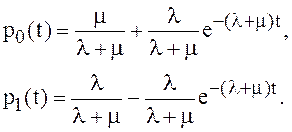 ,
, ![]() , (4)
, (4)
Важнейшими характеристиками системы массового обслуживания являются абсолютная и относительная пропускная способность.
Абсолютная – среднее число заявок, которое система может обслужить в единицу времени; относительная – отношение абсолютной пропускной способности к среднему числу поступивших за это время заявок.
Можно показать, что абсолютная пропускная способность одноканальной системы с отказами в установившемся режиме равна:
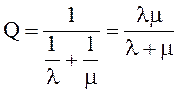 . (5)
. (5)
Тогда относительная пропускная способность равна:
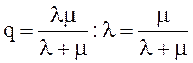 . (6)
. (6)
Видим,
что относительная пропускная способность системы в примере 21 совпадает с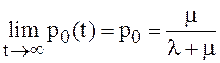 . В этом случае
. В этом случае ![]() является
также пропускной способностью системы в любой момент времени
является
также пропускной способностью системы в любой момент времени![]() :
: ![]() означает,
что в любой момент времени
означает,
что в любой момент времени ![]() канал свободен, а
значит заявка, поступившая в момент времени
канал свободен, а
значит заявка, поступившая в момент времени![]() , будет
обслужена. А это означает, в свою очередь, что
, будет
обслужена. А это означает, в свою очередь, что ![]() есть
отношение числа обслуженных заявок к их общему числу.
есть
отношение числа обслуженных заявок к их общему числу.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.