Однако этот обратный
переход даже в случае скалярного марковского процесса X(t), ![]() , не является однозначным в силу
того, что второе уравнение в (23) имеет бесконечное множество решений. В
практике научных исследований для матричной функции
, не является однозначным в силу
того, что второе уравнение в (23) имеет бесконечное множество решений. В
практике научных исследований для матричной функции ![]() вводят
дополнительное ограничение – матрица
вводят
дополнительное ограничение – матрица ![]() должна быть
симметричной. Это позволяет преобразовать равенство
должна быть
симметричной. Это позволяет преобразовать равенство ![]() в
равенство
в
равенство ![]() , решение которого проще найти (в
вычислительном отношении).
, решение которого проще найти (в
вычислительном отношении).
Пример 2. Пусть
прямое уравнение Колмогорова (11) для условной плотности вероятности ![]() скалярного МП X(t),
скалярного МП X(t), ![]() , имеет вид:
, имеет вид:
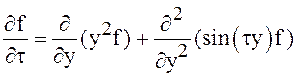 . (24)
. (24)
Согласно обозначениям в уравнении (11) имеем ![]() ,
,![]() . Матрицы диффузии
. Матрицы диффузии ![]() в (11) должны быть неотрицательно
определёнными, следовательно, уравнение (24) определено лишь для
в (11) должны быть неотрицательно
определёнными, следовательно, уравнение (24) определено лишь для ![]() и
и![]() ,
удовлетворяющим требованию
,
удовлетворяющим требованию![]() .
.
Из соотношений (23) следует,
что![]() ,
,![]() . Это значит, что
стохастическое дифференциальное уравнение в форме Ито для СП X(t),
. Это значит, что
стохастическое дифференциальное уравнение в форме Ито для СП X(t), ![]() , имеет вид:
, имеет вид:
![]() , (25)
, (25)
где ![]() –
стандартный винеровский процесс, исходящий из нуля.
–
стандартный винеровский процесс, исходящий из нуля.
Пример 3.
Определим систему стохастических дифференциальных уравнений, которой
удовлетворяет двумерный марковский процесс![]() ),
), ![]() , если условная плотность вероятностей
этого процесса
, если условная плотность вероятностей
этого процесса ![]() удовлетворяет обратному
уравнению Колмогорова:
удовлетворяет обратному
уравнению Колмогорова: 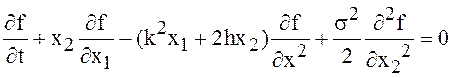 с известными
параметрами
с известными
параметрами ![]() ,
, ![]() и
и![]() .
.
Согласно уравнению (2)
имеем ![]() ,
, ![]() , а также
, а также ![]() ,
, ![]() . Уравнения
(23) дают
. Уравнения
(23) дают
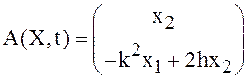 ,
, 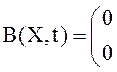
![]() .
.
Тогда система стохастических дифференциальных уравнений (17) может быть представлена в виде:
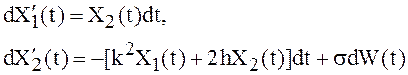
где![]() ,
,
![]() , – стандартный винеровский процесс,
исходящий из нуля.
, – стандартный винеровский процесс,
исходящий из нуля.
Пример 4. Пусть
стохастическая модель состояния в форме Ито имеет вид: ![]() ,
,
![]() .
.
Для определения
коэффициентов сноса и диффузии достаточно воспользоваться равенствами
(23): ![]() ,
, ![]() .
.
Прямое уравнение Колмогорова
для нахождения условной плотности вероятностей ![]() с
учётом замечаний в конце п. 8.2 и того факта, что начальное состояние является
детерминированным, запишем в виде:
с
учётом замечаний в конце п. 8.2 и того факта, что начальное состояние является
детерминированным, запишем в виде:
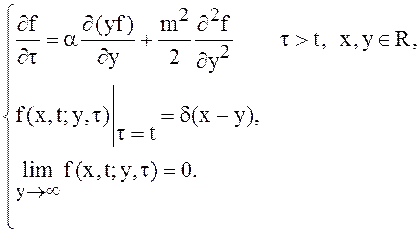 (26)
(26)
Введём обозначение ![]() и запишем характеристическую функцию для
СП X(t),
и запишем характеристическую функцию для
СП X(t),![]() :
:
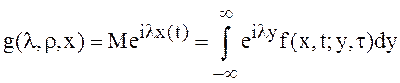 , (27)
, (27)
которая является
преобразованием Фурье условной плотности вероятностей по переменной![]() . В силу (26) и свойств преобразования
Фурье, функция
. В силу (26) и свойств преобразования
Фурье, функция ![]() является решением задачи:
является решением задачи:
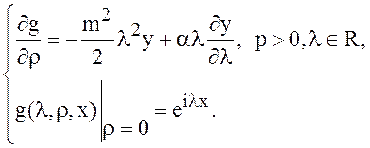
или, что то же самое:
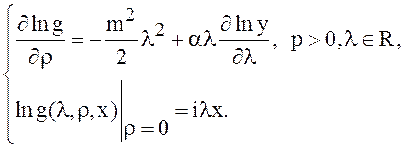
Изображение по Лапласу
функции ![]() (по переменной
(по переменной ![]() ) обозначим
) обозначим
![]() , последняя задача записывается в виде
обыкновенного дифференциального уравнения первого порядка относительно
, последняя задача записывается в виде
обыкновенного дифференциального уравнения первого порядка относительно ![]() :
: 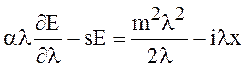 ,
,![]() . Из (26) и свойства функции
. Из (26) и свойства функции ![]() следует, что
следует, что 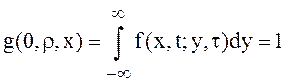 .
Поэтому
.
Поэтому ![]() ,
, ![]()
и 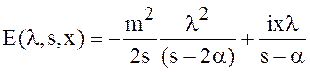 .
По изображению
.
По изображению ![]() находим оригинал вида:
находим оригинал вида:
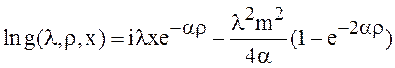 .
.
В правой части получено
выражение для натурального логарифма характеристической функции нормального
распределения с математическим ожиданием ![]() и
дисперсией
и
дисперсией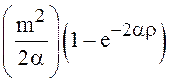 , что значительно упрощает дальнейшие
вычисления. Поэтому выражение для
, что значительно упрощает дальнейшие
вычисления. Поэтому выражение для ![]() можно записать сразу, это
плотность вероятности нормального распределения с указанными параметрами:
можно записать сразу, это
плотность вероятности нормального распределения с указанными параметрами:
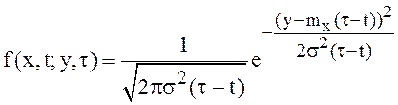 ,
,
где
![]() ,
,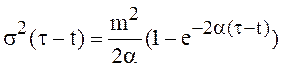 .
.
Иначе пришлось бы по виду ![]() находить
функцию
находить
функцию![]() , затем при помощи обратного преобразования
Фурье находить функцию
, затем при помощи обратного преобразования
Фурье находить функцию![]() .
.
1.
Пусть в стохастической задаче Коши ![]() , n=2,
, n=2,
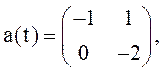
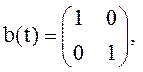
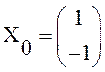 . Определить ковариационную матрицу и м.о. ее решения.
. Определить ковариационную матрицу и м.о. ее решения.
2.
Пусть в стохастической задаче Коши (задача 1) n=2, 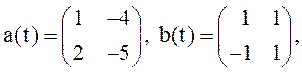
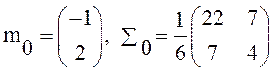 .
Определить м.о., ковариационную матрицу и дисперсионную матрицу ее решения.
.
Определить м.о., ковариационную матрицу и дисперсионную матрицу ее решения.
3.
Найти м.о. и дисперсию стохастического интеграла 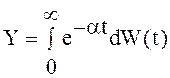 по
стандартному винеровскому процессу, α > 0 - неслучайный параметр.
по
стандартному винеровскому процессу, α > 0 - неслучайный параметр.
4.
Найти м.о. и дисперсию интеграла Ито 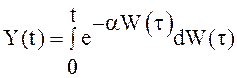 .
.
5.
Найти дисперсию интеграла Ито 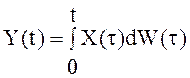 , где
, где ![]() - скалярный СП;
- скалярный СП; 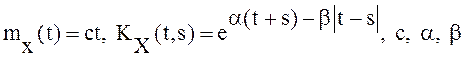 -
неслучайные параметры.
-
неслучайные параметры.
6.
Доказать, что СП ![]() , имеет стохастический
дифференциал в форме Ито
, имеет стохастический
дифференциал в форме Ито ![]() .
.
7.
Доказать, что стохастическое дифференциальное уравнение ![]() имеет
решение
имеет
решение ![]() , удовлетворяющее начальному условию
, удовлетворяющее начальному условию ![]()
8.
Доказать, что стохастическая задача Коши 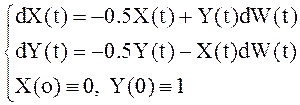 ,
имеет решение
,
имеет решение ![]() .
.
9. Напишите уравнение Чепмена – Колмогорова. Почему оно справедливо лишь для марковских процессов?
10. Можно ли утверждать, что: а) каждая стохастическая модель состояния однозначно определяет СП? б) каждый марковский процесс порожден стохастической системой состояния? в) каждый МП однозначно определяет стохастическую модель состояния?
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.