Анализ цифрового фильтра по заданным значениям его коэффициентов, страница 6

Аналитические выражения импульсной характеристики нерекурсивной части имеет вид:  h_н(0) = b₀=1 ; h_н(1) = b₁=1.73205;  h_н(2) = b₂=1 , а для его рекурсивной части аналитическое выражение импульсной характеристики и в случае простых комплексно-сопряженных полюсов можно привести к виду:

                                                

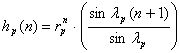
, n = 1, 2, 3,…

Импульсная характеристика всего фильтра является сверткой импульсных характеристик нерекурсивной и рекурсивной части:

  

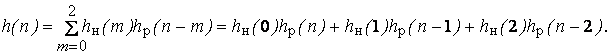
10.Привести графики ИХ нерекурсивной части, рекурсивной части и всего фильтра. Оценить приближенно длительность переходных процессов в фильтре.

 Расчёт импульсных характеристик производился с помощью программы MathCad 2000. Полученные при расчёте графики представлены ниже.

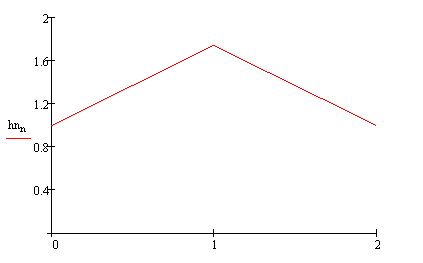
Рис(8). ИХ нерекурсивной части.

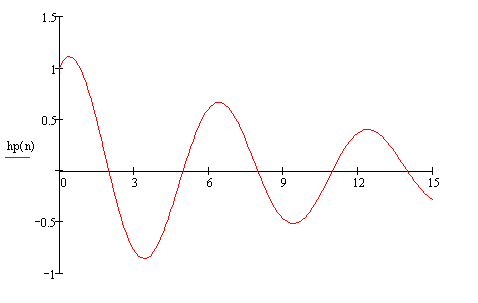
Рис(9). ИХ рекурсивной части.

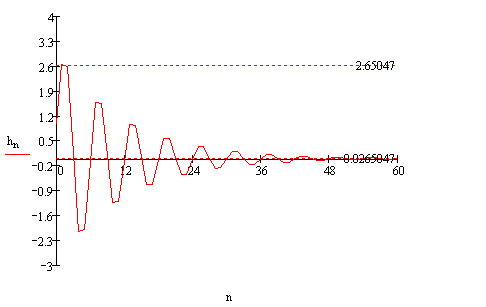
Рис(10). ИХ всего звена.

          Начиная с 56 отсчёта модуль импульсной характеристики не превышает значения 0.0265047, которое примерно в 100 раз меньше наибольшего значения импульсной характеристики поэтому реальную длительность переходного процесса и реальную длительность импульсной характеристики фильтра можно принять равной 56.

          11. В соответствии с разностным уравнением найти отклики фильтра на входные воздействия типа единичный импульс и единичный скачок для n=0, 1,2,…9, построить графики откликов.

          Сигнал на выходе фильтра можно вычислить по разностному уравнению вида:

y(n)=b₀x(n)+b₁x(n-1)+b₂x(n-2)-a₁y(n-1)-a₂y(n-2)

          Отклик фильтра на единичный импульс есть его импульсная характеристика, а отклик фильтра на единичный скачёк есть его переходная характеристика найдём их значения с помощью разностного уравнения для 10 первых точек и построим графики.