Анализ цифрового фильтра по заданным значениям его коэффициентов, страница 13

В алгебраической форме записи.

Z₀₁= 1   Z₀₂= -1

Z_p1= 0.45921+j0.79538     Z_p2= 0.45921-j0.79538  

В показательной форме записи.

Z₀₁=1    Z₀₂=-1

Z_p1=0.91842e^j1.0472     Z_p2=0.91842e^-j1.0472

          Изменение значений нулей фильтра приведёт к изменению его частотных характеристик. Построив соответствующую им картину нулей и полюсов фильтра, можно по ней определить, как изменится его частотная характеристика. В данном случае на частотах l = 0 и l = p будет иметь место бесконечное затухание АЧХ,    т. е. коэффициент передачи, равный нулю.            Отсюда можно сделать вывод, что данный фильтр является полосовым. Для более детального рассмотрения изменения АЧХ фильтра рассчитаем её значения для нескольких точек и построим график.

Рис(15). Картина нулей и полюсов фильтра.

H(l_p)=12.77548 – значение АЧХ на частоте полюса l_p=1.0472.

Рис(16). АЧХ фильтра.

18.Привести граф-схему алгоритма программной реализации звена, оценить требуемый объем памяти и вычислений.

 Выходной сигнал биквадратного звена 2-го порядка можно определить из разносного уравнения вида:

y(n)=b₀x(n)+b₁x(n-1)+b₂x(n-2)-a₁y(n-1)-a₂y(n-2)

          Данному уравнению соответствует граф-схема алгоритма программной реализации РЦФ представленная ниже на Рис(17).

 

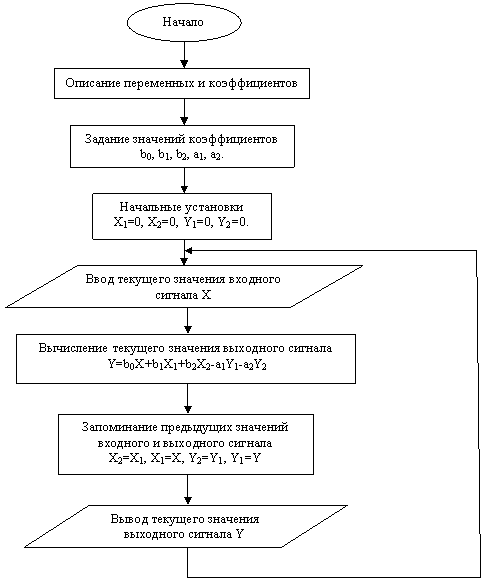Рис(17). Граф – схема алгоритма программной реализации РЦФ на основе биквадратного звена 2-го порядка.

                В граф – схеме алгоритма символами X₁, X₂ Y₁, Y₂ обозначены отсчёты входного и выходного сигнала задержанные на 1 или 2 такта соответственно.