Анализ цифрового фильтра по заданным значениям его коэффициентов, страница 14

          Для реализации данного алгоритма потребуется 4 элемента памяти, 4 операции сложения и 5 операций умножения.

                19. Показать, как по ИХ звена РЦФ реализовать нерекурсивный цифровой фильтр с частотной характеристикой, близкой к частотной характеристике РЦФ. Записать алгоритм обработки для НЦФ (дискретную временную свертку) и требуемый объем памяти и вычислений на один отсчет сигнала. Привести граф-схему алгоритма программной реализации НЦФ.

          Нерекурсивные цифровые фильтры относятся к классу КИХ – фильтров, то есть с конечной импульсной характеристикой. Выходной сигнал таких фильтров можно найти используя выражение для дискретной временной свёртки имеющей конечный предел суммирования, определяемый длинной импульсной характеристики N:

, h(n) – значения импульсной характеристики в дискретных точках.

          Отсюда следует если ограничить ИХ РЦФ конечным числом отсчетов n_p, то по ней можно реализовать НЦФ на основе дискретной временной свертки, осуществляющий обработку сигнала в соответствии с выражением представленным выше, в котором нужно заменить N на n_p. Структура такого фильтра приведена на рис.(18), а на рис.(19),– граф-схема алгоритма его программной реализации. Частотная характеристика такого фильтра определяется выражением:

, h(n) – значения импульсной характеристики в дискретных точках.

ее отличие от частотной характеристики РЦФ будет обусловлено усечением ИХ РЦФ до конечного числа отсчетов n_p.

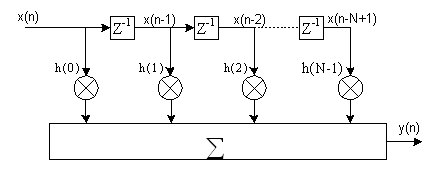Рис(18). Структурная схема НЦФ на основе ДВС.

 

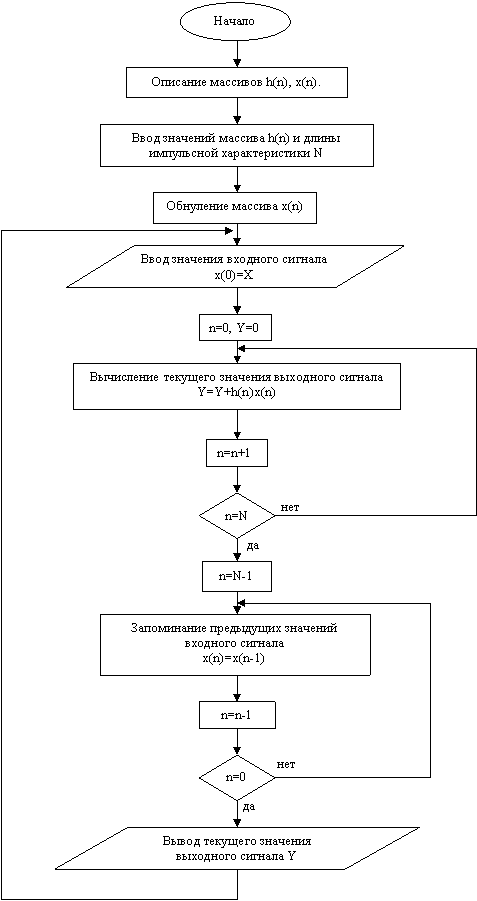
Рис(19). Граф – схема алгоритма программной реализации НЦФ на основе ДВС.

          Для реализации данного алгоритма потребуется N-1 элементов памяти и N операций умножения и сложения.