Анализ цифрового фильтра по заданным значениям его коэффициентов, страница 2

          Ниже приведены схемы для прямой и канонической форм реализации. Символом Z^-1 на схемах обозначены элементы задержки или элементы запоминания сигнала на один период дискретизации Т_Д .

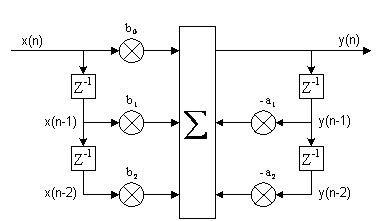
Рис(1).  Структура биквадратного звена при прямой формы реализации.

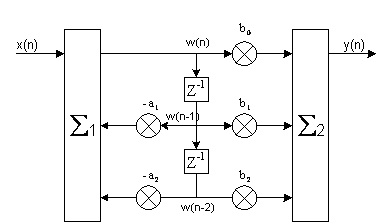
Рис(2). Структурная схема звена для канонической формы реализации.

3.Записать разностные уравнения для обеих форм реализации звена.

Выходной сигнал биквадратного звена 2-го порядка описывается разностным уравнением вида:

y(n)=b₀x(n)+b₁x(n-1)+b₂x(n-2)-a₁y(n-1)-a₂y(n-2)

Данному уравнению эквивалентна пара разностных уравнений вида:

w(n)=b₀x(n)+b₁x(n-1)+b₂x(n-2)

y(n)=w(n)-a₁y(n-1)-a₂y(n-2)

которые раздельно описывают рекурсивную и нерекурсивную части звена при прямой форме реализации.

Разностные уравнения описывающие биквадратное звено 2-го порядка при канонической форме реализации имеют вид:

w(n)=x(n)-a₁w(n-1)-a₂w(n-2)

y(n)=b₀w(n)+b₁w(n-1)+b₂w(n-2)

первое из которых соответствует разностному уравнению рекурсивной, а второе нерекурсивной части звена.

Подставив в эти уравнения значения коэффициентов b₀, b₁, b₂, a₁, a₂. Получим:

w(n)=x(n)+1.73205x(n-1)+x(n-2)

y(n)=w(n)+0.91842y(n-1)-0.8435y(n-2)

w(n)=x(n)+0.91842w(n-1)-0.8435w(n-2)

y(n)=w(n)+1.732053w(n-1)+w(n-2)

Соответственно для прямой, первая пара уравнений, и канонической, вторая пара уравнений  форм реализации.

4. Записать выражения для передаточной функции звена.

Передаточную функцию биквадратного звена 2-го порядка можно представить в виде произведения передаточных функций нерекурсивной и рекурсивной части: . H(z) = H_н(z)H_p(z) , где H_н(z) = b₀ + b₁ z^-1 +b₂ z^-2,                H_p(z) =1/(1 + a₁ z^-1 +a₂ z^-2).