Анализ цифрового фильтра по заданным значениям его коэффициентов, страница 5

Рис(4). График АЧХ.

По виду АЧХ можно сказать что, данный фильтр является фильтром нижних частот.

8.Записать аналитическое выражение для частотной характеристики нерекурсивной, рекурсивной части и всего фильтра и рассчитать их АЧХ для значений нормированной частоты λ в диапазоне от 0 до p. Показать, как они могут быть преобразованы в АЧХ, зависящие от физической частоты f.

Выражения для частотной характеристики получаются из передаточной функции H(z) = H_н(z)H_p(z)  путем замены z на e ^jl :

, где -частотная характеристика нерекурсивной части, а   - частотная характеристика рекурсивной части.

Для получения модуля частотной характеристики |H(jl)| , т. е. АЧХ, нужно воспользоваться формулами: e^-jl = cosl – jsinl ;     

  e^-j2l = cos2l – jsin2l .

          Чтобы получить АЧХ H(f), зависящую от физической частоты f, нужно в выражении для частотной характеристики в место l подставить , и задаться значением частоты дискретизации f_д.

Ниже представлены графики АЧХ нерекурсивной, рекурсивной части и всего звена.

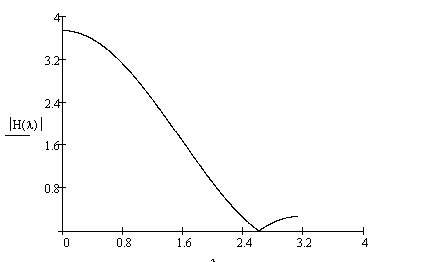
Рис(5). АЧХ нерекурсивной части.

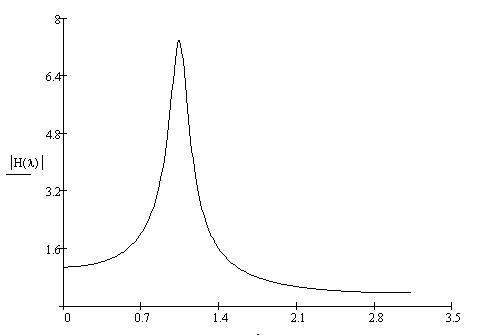
Рис(6). АЧХ рекурсивной части.

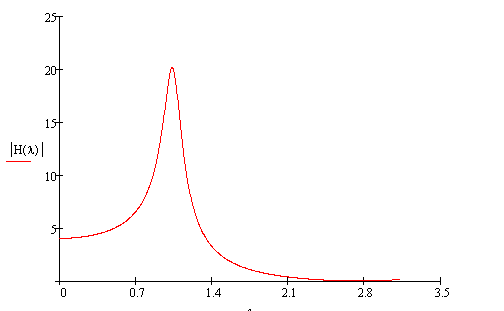
Рис(7). АЧХ всего звена.

                9.Найти аналитические выражения для импульсной характеристики (ИХ) нерекурсивной и рекурсивной частей фильтра, показать, как по ним найти ИХ всего фильтра.