Число
возможных ключей легко варьируется разрядностью функций и может быть
практически неограниченным. Известно, например, что общее количество булевых
функций равно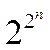 
. Взяв в качестве ключа битовую строку
длиной, скажем, в 5 символов, мы получим количество интегральных функций,
равное 
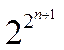, т. е. 18, 446, 744, 073, 709, 551, 616 функций. Не имея в распоряжении
точного алгоритма дифференцирования для определения первичного ключа, т. е.
самой исходной функции, для ее определения необходимо продифференцировать все
это множество функций по каждой из переменной (их в нашем примере 5). Однако
нахождение полного множества интегральных функций для логической функции уже от
5-ти переменных для современных персональных ЭВМ невыполнимая задача, поскольку
не существует даже типов данных, способных хранить такое количество информации,
не говоря уже о размерах оперативной и физической памяти. Уже 10-ти битовый
ключ может гарантировать достаточно низкую вероятность «случайного» подбора
ключа. Дополнительное ограничение времени на сервере после неправильного ввода
ключа для его идентификации и сравнения, к примеру, на 2 минуты, сделает его
подбор практически неосуществимым.
Попытка реализовать нечто подобное была предпринята в последнем программном продукте крупнейшего производителя программного обеспечения, корпорации Майкрософт – Windows XP. Но в связи с допущенными ошибками в программном коде и слабой проработкой степеней его защиты, эта операционная система явилась еще одним ярким примером активной и большинстве случаев успешной деятельности компьютерных пиратов. Результат – в настоящее время Windows XP пополнила длинный список незаконно распространяемых и используемых программных продуктов.
Дифференциал логической функции для различных операций
Дифференциальное исчисление булевых функций нашло большое распространение в жизни человека. Оно помогает решать вопросы, связанные с экспертными системами; задачи по проектированию интегральных схем; позволяет осуществлять оценку переходных процессов в системах и многое другое. При решении ряда задач бывает необходимо разложить функцию на простые подфункции, уменьшить сложность поставленной задачи и т.д., где нам опять помогает дифференциальное исчисление булевых функций. В данной главе на основе расширенного понятия дифференциала рассмотрим ряд теорем, позволяющих эффективно вычислить дифференциал булевой функции для двуместных логических операций дизъюнкция и конъюнкция.
Вспомним определение дифференциала для некоторой двуместной операции p(a,b).
Определение 1.
Дифференциалом логической функции F(xl,x2,...,xn) no переменной xi для операции p(a,b) называется следующее логическое выражение:
∂F(xl,x2,...,xn)
___________ = p(F(xl,x2,...,xi=0,...,xn), F(xl,x2,...,xi=1,...,xn)).
∂xi p
Тогда дифференциал для логических операций имеет вид:
для операции дизъюнкция
∂F(xl,x2,...,xn)
___________ = F(xl,x2,...,xi=0,...,xn) v F(xl,x2,...,xi=1,...,xn)
∂xi v
для операции конъюнкция
∂F(xl,x2,...,xn)
___________ = F(xl,x2,...,xi=0,...,xn) & F(xl,x2,...,xi=1,...,xn).
∂xi &
Рассмотрим свойства дифференциала для основных логических операций. Функцию F(xl,x2,...,xn) = p(fl (xl,x2,...,xn), f2 (xl,x2,...,xn),..., fm (xl,x2,...,xn)) будем называть сложной логической функцией; а fl (xl,x2,...,xn), f2 (xl,x2,...,xn),..., fm (xl,x2,...,xn) – подфункциями функции F(xl,x2,...,xn).
Теорема 1.
Дифференциал для операции дизъюнкция логической функции
F(xl,x2,...,xn)= fl (xl,x2,...,xn) v f2 (xl,x2,...,xn)
равен дизъюнкции дифференциалов
данных функций для операции дизъюнкция:
∂F(xl,x2,...,xn) ∂fl (xl,x2,...,xn) ∂f2 (xl,x2,...,xn)
___________ = ___________ v ___________
∂xk v ∂xk v ∂xk v
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.