Математика \ Математика

Дифференциал и интеграл булевой функции, страница 5

конституэнты поочередно «домножаются» сначала на x n+1, затем на x n+1; они присутствуют в каждой интегральной функции, зависящей от n + 1 переменных и, таким образом, представляют собой как бы «ядро» интеграла для соответствующей логической функции от n переменных. Для каждой такой функции существует добавочный компонент, определяющий число интегральных функций, который представляет собой «нули»                                                                                                                                                                                                                                                                                                                                   

_                                                                                                                                           

подынтегральной функции, домноженные либо на x n+1, либо на x n+1, и, наконец, на 0 (т. е. вообще не присутствуют). Итак, на основе проведенных исследований интеграла для логических функций по операции конъюнкция был определен общий вид интегральных функций для данной операции:

          m                                                        m                                                            m __                                       _ _____

∫  V fi (xl,x2,...,xn)dxn+1 = V fi  (xl,x2,...,xn) & x n+1 v V fi  (xl,x2,...,xn) & x n+1 v

     & i=1                                               i=1                                                    i=1

m                                                                                                                                          

&                                                                                                                                           

… v ∑  fi (xl,x2,...,xn) & x vi n+1 ,

A (v1, v2, …, vm)

_                                                                                                                                           

(   x n+1 ,                     если vi = 0;

где x vi n+1 =  {   x n+1 ,                     если vi = 1; и vi = {0, 1, 2} – все возможные

_                                                                                                                                           

(   (x n+1  v x n+1) = 0, если vi = 2

различные комбинации.

Данная формула верна для любой размерности пространства n, что было проверено с помощью Программного Инструментария.

В ходе исследования интеграла для операции «сложение по модулю 2» оказалось, что количество интегральных функций по данной операции не зависит от вида подынтегральной функции и равно 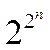, где n — размерность пространства; т. е., если подынтегральная функция зависит от 1 переменной, то количество ее интегральных функций равно = 4; если от двух переменных —  = 24 = 16; от трех —  = 28 = 256 и так далее независимо от переменной интегрирования.

Итак, общий вид интеграла для операции «сложение по модулю 2»

          m                                                                                                                    __                                        _____

∫  V fi (xl,x2,...,xn)dxn+1 = f1  (xl,x2,...,xn) & x φ1 n+1 v f2  (xl,x2,...,xn) & x φ2 n+1 v

     Ө i=1                                                                                                  

k                                   m                                                                                                        

Ө    ^                             ˇ                                                                                                                    

… v fm  (xl,x2,...,xn) & x φm n+1 v ∑  fj  & x ζ1 n+1 = ∑ fi  (xl,x2,...,xn) & x φi n+1 v

j=1                               i=1

A (φ1, φ 2, …, φ m)

k

Ө

… v ∑  fj  & x ζ1 n+1 ,

Скачать файл