В рамках рассмотрения электронной коммерции и распространения программных продуктов через глобальную компьютерную сеть Интернет, будет логично предположить, что пользователь, приобретающий программу, имеет к ней доступ. Опираясь на уже имеющийся опыт в организации защиты информации и современный уровень развития информационных технологий, предлагается следующий подход к защите программного обеспечения с использованием глобальной сети Интернет.
Пользователь, получив программный продукт через сеть, производит оплату через одну из многочисленных систем электронных платежей, после чего получает персональный ключ (например, через e-mail). Этот ключ вводится при первом запуске программы, которая сразу же подключается к серверу производителя данного программного обеспечения и проверяет его на подлинность и уникальность. После этого программа привязывается к конкретному компьютеру (на котором впервые запущена) и не может быть скопирована. В качестве привязки могут быть использованы, к примеру, серийные номера компонентов, компьютера. Ключ, единожды прошедший проверку на сервере, вторично не может быть использован.
Число возможных ключей легко варьируется
разрядностью функций и может быть практически неограниченным. Известно,
например, что общее количество булевых функций равно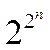 
.
Взяв в качестве ключа битовую строку длиной в n символов, получим количество
интегральных функций, равное 
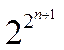. Не имея в распоряжении
точного алгоритма дифференцирования для определения первичного ключа, т. е.
самой исходной функции, для ее определения необходимо продифференцировать все
это множество функций по каждой из переменной. Однако нахождение полного
множества интегральных функций для логической функции уже от 5-ти переменных
для современных персональных ЭВМ невыполнимая задача, поскольку не существует
даже типов данных, способных хранить такое количество информации, не говоря уже
о размерах оперативной и физической памяти. Уже 10-ти битовый ключ может
гарантировать достаточно низкую вероятность «случайного» подбора ключа.
Дополнительное ограничение времени на сервере после неправильного ввода ключа
для его идентификации и сравнения, к примеру, на 2 минуты, сделает его подбор
практически неосуществимым.
Интеграл логических функций для операции дизъюнкция.
Решим задачу нахождения интеграла логических функций для операций дизъюнкция.
На основе понятия интеграла логической функции найдем интеграл логических функций от n переменных для операций дизъюнкция.
Теорема 1.
Множество логических функций интеграла логической функции f(x1,x2,..., xn) для операций дизъюнкция по переменной xn+1 включает следующие логические функции:
_
ò f(x1,x2,..., xn)dxn+1= {f(x1,x2,..., xn); f(x1,x2,..., xn)& xn+1; f(x1,x2,..., xn)& xn+1}
Ú
Доказательство.
¶f(x1,x2,...,
xn)
____________ = f(x1,x2,..., xn) Ú f(x1,x2,..., xn) = f(x1,x2,..., xn);
¶хn+1 Ú
¶(f(x1,x2,...,
xn) & xn+1)
_________________ = 0 Ú f(x1,x2,..., xn) = f(x1,x2,..., xn);
¶хn+1 Ú
_
¶(f(x1,x2,..., xn) & xn+1)
__________________ = f(x1,x2,..., xn) Ú 0 = f(x1,x2,..., xn).
¶хn+1 Ú
Данные преобразования доказывают теорему по основному тождеству интеграла и дифференциала логической функции.
Теорема 2.
Множество логических функций интеграла логической функции f1(x1,x2,..., xn) Ú f2(x1,x2,..., xn) для операций дизъюнкция по переменной xn+1 включает следующие логические функции:
ò (f1(x1,x2,..., xn) Ú f2(x1,x2,..., xn))dxn+1=
Ú
={ f1(x1,x2,..., xn) Ú f2(x1,x2,..., xn)&xn+1; f1(x1,x2,..., xn)&xn+1 Ú f2(x1,x2,..., xn);
_ _
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.