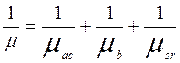(6.35)
где
это подвижность носителей ограниченная
поверхностным рассеянием на акустических фононах, 
-
подвижность носителей в объеме кремния, 
-
подвижность носителей ограниченная рассеянием на шероховатостях поверхности.
Эти вклады описываются следующим образом
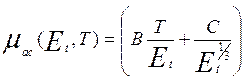(6.36)
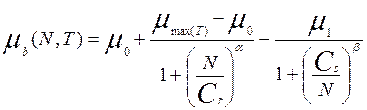(6.37)
где
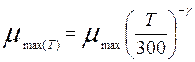, и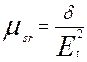 
Основные параметры вышеуказанных выражений определяются пользователем.
6.3 Численные методы
Конечно разностные методы на прямоугольной сетке применяются совместно с разъединенным методом итераций над нелинейностью (так называемые Гуммелевские итерации). Для дискретизации уравнений непрерывности мы использовали общепринятую аппроксимацию Шарфеттера-Гуммеля [11]. Для решения линейных систем применим метод сопряженных градиентов с начальными условиями [12,13]
6.4. Ссылки
[1] М.С. Обрехт ,”SIMOS –программа для двумерного установившегося моделирования МОП приборов”. Твердотельная электроника, Секция обзора программного обеспечения. Том 32, №6, 1989
[2] М.С. Обрехт и ДЖ.М. Тевен “BISIM – программа для установившегося двумерного моделирования различных приборов биполярного типа”. Твердотельная электроника, Секция обзора программного обеспечения. Том 34, №7, 1991
[3] М.С. Обрехт, “ Новый устойчивый метод для линеаризации дискретизируемых основных полупроводниковых уравнений”. Твердотельная электроника, Секция обзора программного обеспечения. Том 36, №4, страницы 643-648, 1993.
[4] М.С. Обрехт и М.И. Элмарси, “Ускорение сходимости Гуммелевских итераций для кратковременного моделирования”. Труды Девятой Международной Конференции по Численному Анализу Полупроводниковых приборов и Интегральных схем. 6-8 апреля, 1993,Front Range Press, страницы 20-21
[5] M. S. Obrecht and M. I. Elmasry, “Speeding-up of convergence of Gummel iterations for transient simulation”, COMPEL, том 12, страница 311-317.
[6] Дж.В. Слотбум и Х.К. Де Граф, “Измерение сужения запрещенной зоны в биполярном кремниевом транзисторе”. Твердотельная электроника, Секция обзора программного обеспечения. Том 19, №4, страницы 857-862, 1976.
[7] А. Г. Чиноветх, “Коэффициенты ионизации для электронов и дырок в кремнии”. Physical Review том 109, страницы 1537-1540, 1958
[8] Д.М. Каугхей и Р.Е. Томас, “Подвижность носителей в кремнии в зависимости от температуры, уровня легирования и инжекции”. Proc.IEEE, том 55, страницы 2192-2193, 1967.
[9] К. Ямагучи,“Модель подвижности носителей в инверсионном слое МОП” IEEE Trans. Электронные приборы, том 30,страницы 658-663, 1983.
[10]К. Ломбарди, С. Манзини, А. Сапорито и М. Ванзи,“Физически основанная модель подвижности для численного моделирования не планарных приборов. IEEE Trans. Computer Aided Design, том 7, страницы 1164-1170, ноябрь 1988.
[11] Д.Л. Шарфеттер, Х.К. Гуммель, “Численное моделирование Осциллятора СВЧ - диода с отрицательным динамическим сопротивлением” IEEE Trans. Electron Devices, vol. 16, страницы 64-70, 1969.
[12] М.С. Обрехт “ Изменение ICCG метода для решения дискретизируемых уравнений непрерывности для полупроводникового прибора при любых напряжениях”. Submitted to Solid State Electronics.
[13] Х.А. Ван Дер Ворст “Bi-CGSTAB:Фиксированный и гладко сходящийся вариант Bi-CG для решения несимметричных линейных систем”. SIAM Journ. Sci. Stat. Comput.,том 13, страницы 631- 644, март 1992.[14] Х.К. Гуммель,”Само-совместимая итерационная схема для одномерного установившегося транзисторного вычисления”. IEEE Trans. Электронные устройства, том.11, страницы 455-465, 1964.
[15] А. Де Мари ”Точное численное установившееся одномерное решение p-n соединения”. Твердотельная электроника, том 11, страницы 33-58, 1968.
[16]М.С. Мокк, “Зависящая от времени численная модель изолированого затвора полевого транзистора”. Твердотельная электроника, том 24, страницы 959-966, 1981.
6.5 Исполнение SemSim
Запуск SemSim из оболочки MicroTec:
§ Выбрать проект, соответствующий SemSim, или добавить новый проект выбрав метод SemSimв окне Method.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.