|
Название |
Текущее значение |
Единицы измерения |
Описание |
|
X0 |
0 |
Мкм |
Координата X верхнего левого угла фрагмента прибора в мкм. Она может превышать длину прибора, если вы хотите инвертировать фрагмент вокруг вертикальной оси симметрии. |
|
SY |
0 |
Нет |
Тип симметрии фрагмента. Если SY=0 то фрагмент не симметричен. SY=1 симметрия вокруг правой грани, так что симметрия распространяется вправо, и SY=-1 симметрия вокруг левой грани, или распространяется в лево. |
|
DX |
0 |
Мкм |
Длина распространения фрагмента, или кусок пригонки между симметричными областями. Значение должно быть больше 0. Игнорируется если SY=0. Эта область заполняется профилем легирования от границ фрагмента. |
|
OV |
1 |
Нет |
Расширение профиля легирования фрагмента на всю область прибора. Это необходимо для создания базовой структуры, например, начальное легирование, имплантация во всю область прибора или скрытый слой. Если OV=1, значение легирования на нижней грани фрагмента продолжается до низа области прибора, и затем профили правого и левого краев фрагмента распространяются неизменно до правого и левого края области прибора соответственно. Если OV=0, фрагмент помещается поверх области, заменяя легированный ранее участок. В этом случае нет никакого расширения вправо, влево, или вниз. Следует выбрать OV=1 для первого фрагмента. |
|
IF |
Название выходного файла SiDif с данными легирования фрагмента. Оно должно быть отделено ‘ ’. |
5.4 Пример входного файла MergIC
Ниже приведен пример входного файла MergIC. Последние три примера различаются только способом расположения фрагментов.
MESH: NX=50 NY=45 XX=5 YY=3, COMM=’Просмотр фрагмента’;
FRAG:X0=0 DX=0 SY=0 OV=1 IF='MOS.OUD'$
MESH:NX=70 NY=40 XX=2.5 YY=1, COMM=’NMOS транзистор’;
FRAG:X0=1.6 DX=0.7 SY=-1 OV=1 IF='EXMOS.OUD'}$
Вертикальный BJT с подложкой - коллектором
MESH:NX=150 NY=40 XX=5 YY=2.5, COMM=’Вертикальный BJT’;
FRAG:X0=4.5 DX=1 SY=0 OV=1 IF='BUR.OUD';}
FRAG:X0=1 DX=1 SY=-1 OV=0 IF='EMIT.OUD';$
Вертикальный BJT со скрытым слоем
MESH:NX=200 NY=40 XX=8 YY=3.5, COMM=’Планарный транзистор’;
FRAG:X0=4. DX=1 SY=0 OV=1 IF='BUR.OUD';}
FRAG:X0=1 DX=1 SY=-1 OV=0 IF='EMIT.OUD';$
Элемент И2Л
MESH:NX=200 NY=40 XX=10 YY=2.5, COMM=’И2Л устройство’;
FRAG:X0=1 DX=1 SY=1 OV=1 IF='BUR.OUD';}
FRAG:X0=10 DX=1 SY=-1 OV=0 IF='EMIT.OUD';$
6.1 Введение
В настоящее время доступно множество программ для двумерного моделирования полупроводниковых приборов. Эти программы используют Ньютоновские методы и это приводит к численной неустойчивости и относительно высоким требованиям к памяти.
Недавно были опубликованы [3,4,5] новые методы линеаризации полупроводниковых уравнений, позволяющие эффективно решать их. Эти методы используют “разъединенную” или Гуммелевскую схему [14] , значительно снижающую требования к памяти. Эти методы оказались более эффективными и численно более устойчивыми, чем Ньютоновские.
SemSim так же как и предшествующие программы SiMOS [1] и BiSim [2] основан на методе Гуммелевского разъединения и требует около 4 Кб памяти для 10.000 узлов сетки. Используется метод конечной разности на прямоугольной сетке. Для дискретизации уравнений непрерывности используется общепринятое приближение Шарфеттера-Гуммеля. Для решения линейных систем применяются методы сопряженных градиентов с предварительными условиями [12,13].
6.2 Фундаментальная система уравнений.
Основные уравнения включают в себя (в стандартных обозначениях) уравнение Пуассона и уравнения непрерывности для электронов и дырок
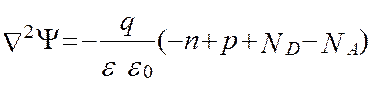 , (6.1)
, (6.1)
 ,
(6.2)
,
(6.2)
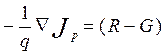 ,
(6.3)
,
(6.3)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.