MicroTec 3.02:Руководство пользователя (МicroTec: Полупроводниковый TCAD калькулятор. Интерфейс пользователя MicroTec. Графика MicroTec: SibGraf), страница 16

где ,и  обозначают плотности токов и электростатический потенциал.

,                           (6.4)

,                           (6.5)

Сужение запрещенной зоны

Дополнительный вклад в дрейфовые компоненты вызван сужением запрещенной зоны и рассматривается в соответствии с моделью Slotboom [6]

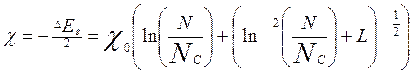,                (6.7)

где .

Температурная зависимость ширины запрещенной зоны выглядит следующим образом:

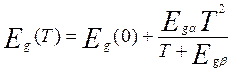.                                (6.8)

Собственная концентрация носителей:

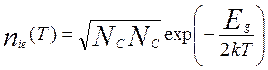.                         (6.9)

Эффективная плотность состояний:

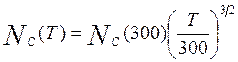.                                 (6.10)

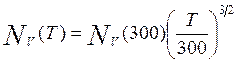.                                 (6.11)

Рекомбинация Шокли-Рида-Холла, Оже рекомбинация и ударная ионизация.

Рекомбинация Шокли-Рида-Холла, Оже рекомбинация и лавинная ионизация из формул:

,                               (6.12)

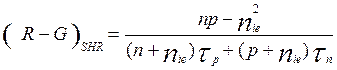,                                      (6.13)

,                                      (6.14)

Используется концентрационная зависимость времени жизни

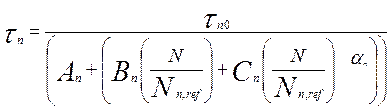                           (6.15)

И аналогичное выражение для дырок.

Ударная ионизация смоделирована  с помощью модели Chynoweth [7]

,                                                           (6.16)

где

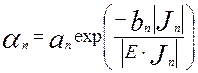       и 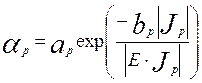                   (6.17)

Поверхностная рекомбинация

Поверхностная рекомбинация имеет место на поверхности раздела полупроводника/окисла или на поверхности неидеальных контактов (например, поликремний или диод Шотки). Скорость рекомбинации описана формулой

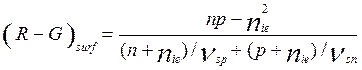,                                  (6.18)

где , скорость рекомбинации для электронов и дырок.

Граничные условия

В SemSim доступны несколько типов граничных условий. В идеальных омических контактах использованы следующие условия (принята бесконечная скорость рекомбинации для электронов и дырок)

,                                       (6.19)

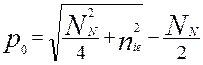,                                       (6.20)

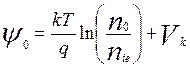,                                      (6.21)

где результирующая концентрация легирования и напряжение К-го контакта.

На поверхности контактов Шотки  (только для BiSim) концентрация носителей определяется следующими соотношениями

,                                                     (6.22)

,                                                   (6.23)              

-                                                                                                     (6.24)

где Ф_B разность работ выхода собственного полупроводника и металла, n определяет плотность компонент тока нормально к поверхности раздела и равновесные концентрации n_eq, p_eq.

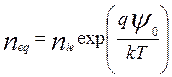,                                                    (6.25)

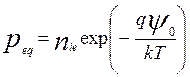,                                               (6.26)

Для изолированных сегментов на границе для плотности тока мы имеем

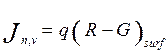,                                                 (6.27)

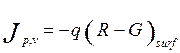.                                               (6.28)

Для нормальных компонент электрического поля на границах раздела согласно теореме Гаусса мы имеем

                                              (6.29)     

где диэлектрические проницаемости соответствующих материалов и фиксированная поверхностная плотность заряда. Для открытых граничных сегментов  равняется нулю. Для граничных сегментов под контактами затвора электрическое поле аппроксимируется формулой

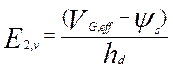                                               (6.30)  

где , толщина окисла и  локальное значение потенциала на границе раздела.

Модели подвижности

Доступны некоторые опции в зависимости подвижности от концентрации и электрического поля. Для биполярных устройств эти зависимости описываются аналогично [8].

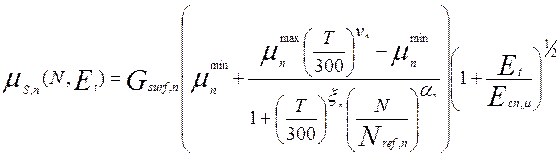           (6.31)

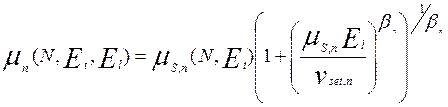                                  (6.32)

и аналогичное выражение для дырок.

Для МОП устройств применяются как выражения Ямагучи [9] так и соответствующие выражения Ломбарди и др.[10]. В первом случае [9]

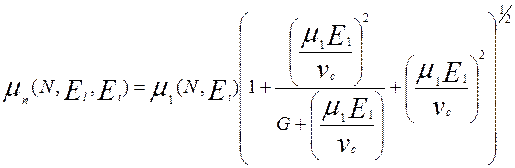                    (6.33)

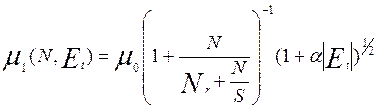                                                (6.34)

где E_l и E_t соответственно продольные и поперечные составляющие электрического поля относительно направления тока. Во втором случае [10] подвижность включает в себя три составляющих