Эта модель использует квазинейтральную аппроксимацию, которая связыват электрическое поле с концентрацией примеси.
где
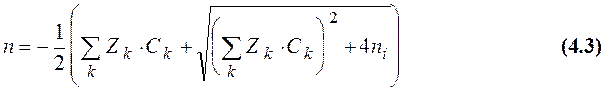Здесь n концентрация электронов и ni собственная
концентрация носителей.
Из (2) и (3) мы имеем
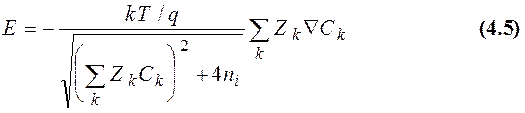
Полагая, что справедливо соотношение Эйнштейна
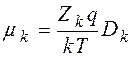
, уравнение диффузии преобразуется в
В случае одной примеси дрейф может быть учтён
введением домножаемого коэффициента для коэффициента диффузии [3], в то время,
как для нескольких примесей следует решать систему связанных уравнений
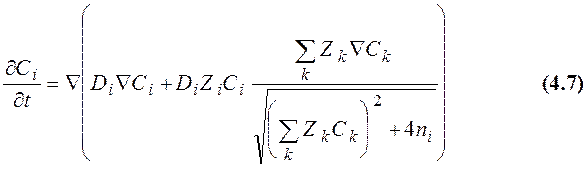
Коэффициент диффузии
Коэффициент диффузии мышьяка и бора, связанный с влиянием однозарядных дефектов, выбирается в форме [3,4,5]
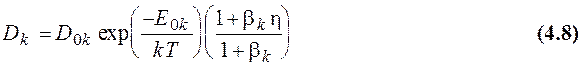где
h = n/ni для мышьяка,
h = p/ni для бора,
D0k - собственный коэффициент диффузии,
E0k - энергия активации k-й примеси,
bk = 3 для бора и 100 для мышьяка.
Коэффициент диффузии фосфора выбран в виде [5,6] и объясняется влиянием нейтральных, одно и двухкратно отрицательно заряженных вакансий.
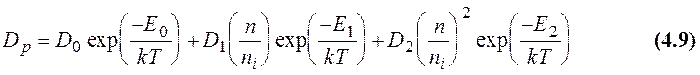
Диффузия, ускоренная окислением
Коэффициент диффузии во время окисления изменяется в зависимости от скорости окисления для того, чтобы описать диффузию, ускоренную (замедленную) окислением [8]. Окисление изменяет коэффициент диффузии потому, что она cоздаёт промежуточные дефекты в кристаллической решётке. В SiDif используется модель Танигучи [8].
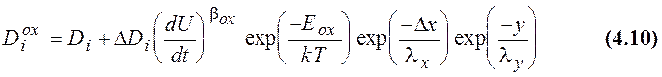Ускорение диффузии экспоненциально убывает в верхней
формуле, где
Dx - расстояние от края маски (Dx = 0 вне области маски) и
y - вертикальное расстояние от границы раздела [8].
Аналитическая модель окисления
Для аналитической модели окисления в SiDif используется модель Дила-Гроува [7].
где U - толщина окисла, А и В - кинетические
константы, которые пропорциональны давлению и зависят от состава окружающей
среды. Значения А и В значительно больше в присутствии паров воды или HCl.
В последнем случае константы берутся из [16,17].
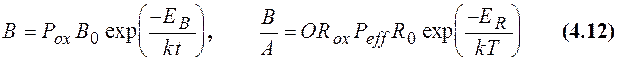где
Pox - давление окислительной среды в атмосферах и Peff - эффективное давление для линейного кинетического коэффициента В/А. В случае влажного окисления Peff = Pox, а в случае сухого Peff = Poxbp. Коэффициент ORox зависит от ориентации кремния [17].
Если имеется начальная окисная плёнка с толщиной U0 на поверхности полупроводника, то из (4.11) следует
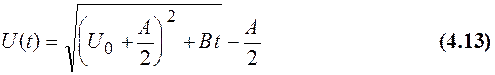Обычно только небольшая часть поверхности подложки
находится в окислительной среде, в то время как остальная поверхность покрыта
нитридной маской. В этом случае окисление у краёв маски описывается формулой
"птичьего клюва"
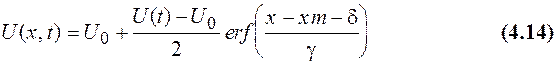
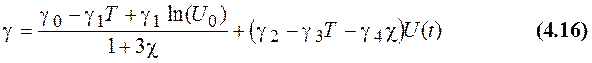со следующими эмпирическими
параметрами [10]
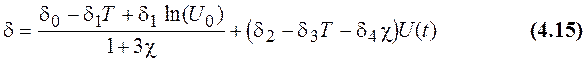
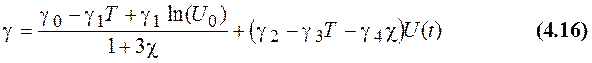
где c = 1 или 0 для ориентации (111) и (100) соответственно.
СЕГРЕГАЦИЯ
Окисление в кремнии сопровождается сегрегацией, другими словами, скачком концентрации примеси на движущейся границе Si/SiO2. Сегрегация обусловлена потоком плотности принеси на границе, который может быть записан как
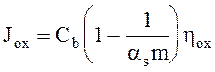(4.17)
где: Сb - концентрация примеси в Si на границе с SiO2,
m - коэффициент сегрегации,
nox - скорость роста окисла в направлении, перпендикулярном границе,
s -
отношение объёмов Si и SiO2, которое равно 0,44
Для бора:
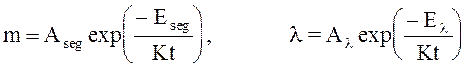(4.18)
Для фосфора и мышьяка коэффициент сегрегации большой (около 100) и обычно близок к равновесной величине [II], так что можно принять, что примесь полностью выталкивается в Si. В этом случае:
J0x = Cbnox (4.19)
При больших скоростях окисления сегрегация может стать причиной того, что с обеих сторон границы концентрации не достигают равновесных величин. В этом случае была предложена поправка [10]
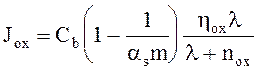(4.20)
где:
- кинетическая константа реакции сегрегации. Равновесные значения m
были взяты из [9].
ИОННАЯ ИМПЛАНТАЦИЯ (И.И)
И.И. сейчас широко используется как стандартный метод легирования п/п пластин. В SiDif реализована аналитическая модель ионной имплантации.
В одномерном случае имплантация описывается распределением Гаусса.
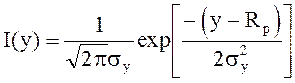(4.21)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.