Информатика и выч. техника \ Применение ЭВМ в электротехнических расчетах

Рабочая программа, методические указания и контрольные задания по дисциплине «Применение ЭВМ в электротехнических расчетах», страница 9

Если , то возможны два случая:  меняет знак на отрезке [x1; xM] () или на отрезке [xM; x2] (). Выбирая в каждом случае тот из отрезков, на котором  меняет знак, и, продолжая процесс половинного деления по зависимости (9) дальше (т.е. принимая  или ), можно дойти до сколь угодно малого отрезка, содержащего корень.

Итерационный процесс прекращается при выполнении условия

 или                                (10)

где ε – заданная точность решения уравнения.

Метод хорд. Аналогичен методу дихотомии, но в качестве приближения к корню уравнения принимаем значение  точки пересечения хорды, проведенной через точки  и , с осью абсцисс:

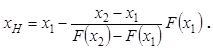                             (11)

Условие прекращения итерационного процесса аналогично (10), только вместо значения  подставляется .

Метод Ньютона. Отличие от предыдущего метода состоит в том, что на каждой итерации вместо хорды проводится касательная к кривой  в точке  (где  – начальное приближение к значению корня) и ищется точка пересечения касательной с осью абсцисс. Полученное при этом значение  используется в качестве начального приближения на следующей итерации, т.е. . Общая формула имеет вид

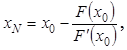                                                   (12)

где  – значение производной в точке .

Итерационный процесс прекращается при выполнении условия

 или                                (13)

В качестве начального приближения на первой итерации можно принять середину отрезка [a; b], т.е. .

Ниже приведен текст программы на языке Паскаль.

Program RU1OK;

{ Решение уравнений с одной переменной.

  Метод отделения корней }

Vara,b,a1,b1,h:real;

Function F(x:real):real;

begin

 F:=x-10*sin(x);

end;

begin

write ('Интервал поиска корней a,b=,

      шаг отделения корней h=');

readln (a,b,h);

     a1:=a; b1:=a1+h;

   while b1<=b do

   begin

      if F(a1)*f(b1)<=0 then

      writeln('Корень принадлежит области ',a1:7:4,

'   ',b1:7:4);

   a1:=b1;

   b1:=a1+h;

   end;

   readln;

end.

ProgramRU1D;

{ Решение уравнений с одной переменной.

  Методдихотомии}

Const E=0.0001;

Var a,b,x1,x2,xc:real; { xc = xM }

Function F(x:real):real;

begin

 F:=x-10*sin(x);

end;

begin

     write ('Интервал поиска корня a,b=');

     readln (a,b);

     x1:=a; x2:=b;

     xc:=(x1+x2)/2;

   while abs(F(xc))>E  do

   begin

      if F(xc)*F(x2)<=0 then  x1:=xc else x2:=xc;

      xc:=(x1+x2)/2;

   end;

      writeln('Корень=',xc:7:4);

readln;

end.

ProgramRU1hord;

{ Решение уравнений с одной переменной.

  Методхорд}

Const E=0.0001;

Var a,b,x1,x2,xc:real; { xc = xH }

Function F(x:real):real;

begin

 F:=x-10*sin(x);

end;

begin

     write ('Интервал поиска корня a,b=');

         readln (a,b);

     x1:=a; x2:=b;

     xc:=x1-(x2-x1)/(F(x2)-F(x1))*F(x1);

   while abs(F(xc))>E  do

   begin

      if F(xc)*F(x2)<=0 then  x1:=xc else x2:=xc;

      xc:=x1-(x2-x1)/(F(x2)-F(x1))*F(x1);

   end;

      writeln('Корень=',xc:7:4);

   readln;

end.

ProgramRU1Nuton;

{ Решение уравнений с одной переменной.

  Метод Ньютона }

ConstE=0.0001;

dx=0.0001;

Var a,b,x0,x,Fpr:real; { x = xN }

    n:integer;

Function F(x:real):real;

begin

 F:=x-10*sin(x);

end;

begin

write (' Начальное приближение a=');

readln (a);

     x:=a;

     n:=0;

 repeat x0:=x;

        n:=n+1;

        if n>30000 then halt;

       Fpr:=(F(x0+dx/2)-F(x0-dx/2))/dx;

       x:=x0-F(x0)/Fpr

 until  abs(x-x0)<E;

      writeln('Корень=',x:7:4);

      readln;

end.

Задание 4

Задание 4 имеет учебной целью закрепление пройденного материала по теме «Линейные системы и методы решения. Прямые методы. Метод Гаусса».

Условие задания 4. Решить систему трех линейных алгебраических уравнений

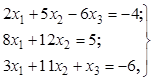
методом Гаусса.

Алгоритм выполнения задания. Метод Гаусса состоит из двух этапов.

1. Прямой ход. Преобразовываем матрицу системы к треугольному виду путем последовательного исключения неизвестных из уравнений. Последовательное исключение выполняется  раз, где  – количество уравнений системы. Общие зависимости для нахождения коэффициентов преобразованных матриц имеют вид

Скачать файл