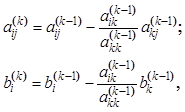Рабочая программа, методические указания и контрольные задания по дисциплине «Применение ЭВМ в электротехнических расчетах», страница 10

                                          (14)

где  – номер неизвестного, которое исключается из оставшихся  уравнений (а также номер того уравнения, с помощью которого исключается );  – номер уравнения, из которого исключается неизвестное;  – номер столбца.

Таким образом, прямой ход метода Гаусса состоит из трех вложенных циклов. Внешний цикл по k – организация  преобразования для исключения неизвестных; средний и внутренний циклы по i и j – организация вычислений коэффициентов системы на каждом k-м преобразовании.

2. Обратный ход. Сначала находим из последнего уравнения системы неизвестное :

                                             (15)

Затем последовательно находим неизвестные  по зависимости

                          (16)

где  – номер неизвестного, которое определяется из i-го уравнения;  – номера уже найденных неизвестных.

В процессе исключения неизвестных необходимо выполнять операции деления на диагональные коэффициенты , поэтому они должны быть отличны от нуля. В противном случае необходимо переставить уравнения системы.

Ниже приведен текст программы на языке Паскаль.

Program Gauss;

{Решение системы линейных алгебраических уравнений методом Гаусса}

const n=3;

a:array [1..n,1..n] of real=

((2,5,-6),(8,12,0),(3,11,1));

b:array [1..n] of real=(-4,5,-6);

var i,j,k:integer;

    c,S:real;

    x:array [1..n] of real;

begin

  for k:=1 to n-1 do

   for i:=k+1 to n do

   begin c:=a[i,k]/a[k,k];

         a[i,k]:=0;

         for j:=k+1 to n do

         a[i,j]:=a[i,j]-c*a[k,j];

         b[i]:=b[i]-c*b[k];

   end;

  for i:=1 to n do

   begin for j:=1 to n do write (' ',a[i,j]:5:2);

         write (' ',b[i]:5:2);writeln;

   end;

  x[n]:=b[n]/a[n,n];

  for i:=n-1 downto 1 do

  begin S:=0; for j:=i+1 to n do

              S:=S+a[i,j]*x[j];

        x[i]:=(b[i]-S)/a[i,i];

  end;

  for i:=1 to n do writeln(' x',i,'=',x[i]:6:3);

  readln;

end.

Задание 5

Задание 5 имеет учебной целью закрепление пройденного материала по теме «Нелинейные системы и методы решения. Метод Ньютона».

Условие задания 5. Решить систему нелинейных уравнений

методом Ньютона с заданной точностью =0,0001. Начальные приближения  равны .

Алгоритм выполнения задания. Для разработки программы на языке Паскаль введем следующие обозначения. Пусть необходимо решить систему n нелинейных уравнений для нахождения неизвестных  

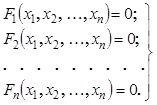                                            (17)

Метод Ньютона основан на разложении функций  в ряд Тейлора, причем члены, содержащие производные второго и более высокого порядков, отбрасываются.

Обозначим приближенные значения неизвестных системы соответственно . Задача состоит в нахождении приращений к этим значениям , благодаря которым решение системы запишется в виде

                 (18)

Разложив левые части уравнений с учетом (18) в ряд Тейлора, получаем следующую систему линейных алгебраических уравнений относительно :

                           (19)

Значения функций  и их частных производных  вычисляются при .

Таким образом, итерационный процесс решения системы уравнений сводится к решению системы линейных алгебраических уравнений (19) для нахождения  и последующему определению  по зависимости (18). Принимая после каждой итерации , продолжаем вычисления до выполнения условия

                                          (20)

где ε – заданная точность решения системы.

Ниже приведен текст программы на языке Паскаль.

Program SNUR_N;

{Решение системы нелинейных алгебраических

 уравнений методом Ньютона}

const n=2;e=0.0001;

type  mas=array [1..n] of real;

      mas1=array [1..n,1..n] of real;

      fun=function(x:mas):real;

var   ja:mas1;

      b:mas;

      x,dx:mas;

      i,j,ki:integer;

      dxmax:real;

{Функции левых частей системы (17)}

function f1(x:mas):real;

begin f1:=x[1]-sqr(x[2]);

end;

function f2(x:mas):real;

begin f2:=10*ln(x[1])+x[2]-10;

end;

{Функции частных производных }

function f11(x:mas):real;

begin f11:=1;

end;

function f12(x:mas):real;