Рабочая программа, методические указания и контрольные задания по дисциплине «Применение ЭВМ в электротехнических расчетах», страница 7

Порядок выполнения работы

1. Составить программу вычисления коэффициентов Фурье.

2. Ввести исходные данные: количество гармонических составляющих , функцию, точность вычисления определенного интеграла .

3. Найти коэффициенты  и .

4. Сравнить графики функции  и функции, полученной в результате синтеза Фурье. На основании этого сравнения сделать выводы о точности представления заданной функции рядом Фурье.

3. ПРИМЕРЫ ВЫПОЛНЕНИЯ ЗАДАНИЙ

Задание 1

Задание 1 имеет учебной целью закрепление пройденного материала по теме  «Интерполяция функций многочленом Лагранжа».

Условие задания 1. Получить значение функции , заданной таблицей 8, в точке , где  при помощи интерполяционного многочлена Лагранжа.

Таблица 8 – Функция, заданная в табличном виде

Алгоритм выполнения задания. Построение многочлена Лагранжа относится к методам глобальной интерполяции (интерполяционный многочлен един для всего интервала [x₀; x_n]). Многочлен Лагранжа позволяет интерполировать таблицы с неравномерным шагом аргумента и легко реализуется на ЭВМ. Обычно его записывают в следующем виде:

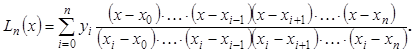              (1)

В случае выполнения расчетов на ЭВМ нет необходимости раскрывать скобки и производить возведение в степень, а достаточно произвести перемножение соответствующих сомножителей, что повышает точность расчетов. В этом случае основная рабочая часть программы состоит из двойного цикла – во внутреннем цикле вычисляются  значений многочленов-слагаемых  вида

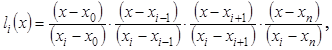                     (2)

а во внешнем цикле накапливается общая сумма

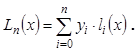                                        (3)

Ниже приведен текст программы на языке Паскаль.

Program Lagranzh;

{ Интерполяция функций с использованием многочлена Лагранжа}

const n=4;

 x:array [0..n] of real=(1.5,3.5,5.5,7.5,9.5);

 y:array [0..n] of real=

        (1.047,46.283,-6.887,14.492,42.236);

var L,p1,p2,xv:real;

    i,k:integer;

begin write ('Введите значение точки a=');

readln (xv);

      L:=0;

      for i:=0 to n do

  begin p1:=1; p2:=1;

        for k:=0 to n do

         if i<>k then

              begin p1:=p1*(xv-x[k]);

                    p2:=p2*(x[i]-x[k]);

              end;

        L:=L+y[i]*p1/p2;

  end;

  writeln('L(',xv:7:3,')=',L:7:3);

  readln;

end.

Задание 2

Задание 2 имеет учебной целью закрепление пройденного материала по теме  «Численное интегрирование. Метод прямоугольников. Метод трапеций. Метод Симпсона».

Условие задания 2. Вычислить значение определенного интеграла

по формулам прямоугольников, трапеций и Симпсона с точностью =0,00001.

Алгоритм выполнения задания.

Метод прямоугольников  состоит в вычислении  интегральной суммы. При этом площадь фигуры, ограниченной функцией , складывается из площадей элементарных прямоугольников ; ; где ;  – количество элементарных участков разбиения отрезка [a; b]. В результате график функции  представляется в виде ступенчатой функции, состоящей из  ступеней. Расчетная формула метода прямоугольников записывается в следующем виде:

                                                 (4)

где h – шаг интегрирования, . Очевидно, при возрастании  ступенчатая функция приближается к функции . Степень необходимого приближения, т.е. количество участков разбиения  определяется заданной точностью .

Метод трапеций основан на линейной интерполяции, т.е. график функции  представляется в виде ломаной, соединяющей точки : ; . В этом случае площадь всей фигуры складывается из площадей элементарных трапеций. Расчетная формула метода трапеций записывается в следующем виде:

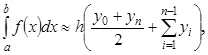                                   (5)

где h – шаг интегрирования, .

Метод Симпсона основан на квадратичной интерполяции, т.е. на каждом отрезке подынтегральная функция  заменяется многочленом второй степени. Расчетная формула метода Симпсона имеет вид

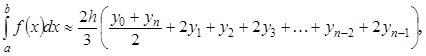      (6)

где n – четное число.