Рабочая программа, методические указания и контрольные задания по дисциплине «Применение ЭВМ в электротехнических расчетах», страница 12

Условие задания 7. Разложить функцию

на отрезке  [-π, π] в ряд Фурье. Количество гармонических составляющих задать параметром .

Алгоритм выполнения задания. Для разработки программы на языке Паскаль введем следующие обозначения. Ряд Фурье для абсолютно интегрируемой на отрезке [-π, π] функции  обозначим следующий ряд:

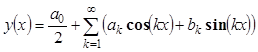,                                (25)

где  и  – коэффициенты Фурье.

Алгоритм спектрального анализа функции  на основе ряда Фурье (25) на отрезке [-π, π] состоит в нахождении коэффициентов Фурье по формулам Эйлера-Фурье:

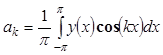;                                         (26)

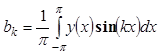.                                          (27)

Вычисление определенного интеграла в (26) и (27) оформим отдельной функцией по методу Симпсона, а подынтегральные функции будем формировать в зависимости от переменной  и параметра , значение которого выбирается произвольным. Очевидно, чем больше количество гармоник , тем более точное представление функции  рядом Фурье.

Ниже приведен текст программы на языке Паскаль.

Program FURJE;

{ Разложение функции F(x) в ряд Фурье.

  Вычисление коэффициентов Фурье ak, bk}

Const E=0.0001;

       N=100;

Type  fun=function (x:real):real;

Var a,b,Integ:real;

    k,m:integer;

    ak,bk:array [0..N] of real;

{ Функция разложения в ряд Фурье}

Function F(x:real):real;

begin F:=exp(-x)*sin(x);

end;

{ Интегрирование методом Симпсона}

Function IntegSim(a,b,E:real;fx:fun):real;

Var I,Ip,dI,h,S1,S2:real;

    j,n:integer;

begin

     Ip:=100*E;n:=100;

   repeat

         n:=n+2;

         h:=(b-a)/n;

         S1:=0; S2:=0;

         For j:=1 to n-1 do

             if j mod 2=1 then S1:=S1+fx(a+j*h)

                          else S2:=S2+fx(a+j*h);

         I:=h/3*(fx(a)+fx(b)+4*S1+2*S2);

         dI:=abs(I-IP);

         Ip:=I

   until dI<E;

   IntegSim:=I;

end; {IntegSim}

{$F+}

Function F1(x:real):real;

begin F1:=F(x)*cos(k*x);

end;

Function F2(x:real):real;

begin F2:=F(x)*sin(k*x);

end;

{$F-}

{основная программа}

begin

Write (' Количество гармоник = ');

readln (m);

  For k:=0 to m do

  begin ak[k]:=IntegSim(-pi,pi,E,F1)/pi;

        bk[k]:=IntegSim(-pi,pi,E,F2)/pi;

        writeln (' ak',k,'=',ak[k]:8:4,

                 ' bk',k,'=',bk[k]:8:4);

  end;

  readln;

end.

список литературы

1. Заварыкин В.М., Житомирский В.Г., Лапчик М.П. Численные методы. – М.: Просвещение, 1991. – 176 с.

2. Зуев Е.А. Язык программирования Turbo Pascal 6.0, 7.0. – М.: Веста, Радио и связь, 1993. – 384 с.

3. Крылов В.И., Бобков В.В., Монастырный П.И. Вычислительные методы: В 2 т. – М.: Наука, 1976. – Т.1 – 304 с. – Т.2 – 400 с.

4. Мудров А.Е. Численные методы для ПЭВМ на языках Бейсик, Фортран и Паскаль. – Томск: МП "Раско", 1991 – 272 с.

5. Турчак Л.И. Основы численных методов. – М.: Наука, 1987. – 320 с.

6. Арфкен Г. Математические методы в физике. – М.: Наука, 1970. – 296 с.

Навчальне видання

РОБОЧА ПРОГРАМА. МЕТОДИЧНІ ВКАЗІВКИ

 ТА КОНТРОЛЬНІ ЗАВДАННЯ

з дисципліни «Використання ЕОМ в електротехнічних розрахунках»

для студентів спеціальності 07.092201 «Електричні системи

і комплекси транспортних засобів» заочної форми навчання

Російською мовою

Укладачі:    ВОЛОНЦЕВИЧ Дмитро Олегович

КОСТЯНИК Ірина Віталіївна

СЄРИКОВ Володимир Іванович

УСТИНЕНКО Олександр Віталійович

Відповідальний за випуск проф. Є.Є. Александров

Роботу рекомендував до видання проф. В.К. Бєлов

В авторській редакції

Комп’ютерне верстання                                   І..В. Костяник

План 2007 р., поз.

Підп. до друку _____________. Формат 60´84 1/16. Папір офсетний. Друк – ризографія. Гарнітура Times New Roman. Ум. друк. арк.    . Обл. вид. арк.    . Тираж 50 прим. Зам. №_____. Ціна договірна.