Математика \ Математические модели

Элементы сетевого планирования и управления (Варианты заданий к расчетно-графическим работам), страница 5

 № 4 Задача минимизации издержек производства методом наискорейшего спуска

Требуется:

1) Постановка задачи;

2) Решить задачу методом наискорейшего спуска;

3) Сделать вывод.

1. Постановка задачи. Предприятие выпускает два вида продукции в объемах x1 и x2 (x1 и x2 могут быть усредненными значениями).

Функция f(x1, x2) =   (усл. ден. ед.) определяет себестоимость производства продукции. Улучшить начальный план 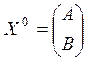 производства продукции с целью минимизации издержек производства. Решить задачу, используя метод наискорейшего спуска, выполнив две итерации вычислительного процесса.

Задача минимизации издержек производства методом наискорейшего спуска

Варианты № 1-30

№ вар.

Целевая функция

Начальное приближение

1.   

(9; 7)

2.   

(8; 9)

3.   

(9; 6)

4.   

(11; 7)

5.   

(10; 6)

6.   

(9; 10)

7.   

(8; 8)

8.   

(10; 9)

9.   

(11; 10)

10.   

(5; 12)

11.   

(8; 10)

12.   

(6; 13)

13.   

(13; 9)

14.   

(9; 14)

15.   

(9; 16)

16.   

(7; 10)

17.   

(8; 14)

18.   

(9; 17)

19.   

(8; 16)

20.   

(7; 19)

21.   

(7; 5)

22.   

(9; 4)

23.   

(11; 3)

24.   

(10; 2)

25.   

(9; 3)

26.   

(8; 7)

27.   

(5; 13)

28.   

(9; 10)

29.   

(6; 13)

30.   

(9; 18)

Задача минимизации издержек производства методом наискорейшего спуска

Варианты № 31-60

№ вар.

Целевая функция

Начальное приближение

31.   

(10; 6)

32.   

(9; 8)

33.   

(10; 5)

34.   

(12; 6)

35.   

(13; 5)

36.   

(10; 9)

37.   

(9; 7)

38.   

(11; 8)

39.   

(12; 9)

40.   

(6; 11)

41.   

(9; 11)

42.   

(7; 12)

43.   

(14; 8)

44.   

(10; 13)

45.   

(10; 15)

46.   

(9; 9)

47.   

(9; 15)

48.   

(10; 16)

49.   

(9; 15)

50.   

(8; 18)

51.   

(8; 4)

52.   

(10; 5)

53.   

(12; 4)

54.   

(11; 3)

55.   

(8; 4)

56.   

(9; 6)

57.   

(6; 12)

58.   

(8; 11)

59.   

(7; 12)

60.   

(8; 17)
Скачать файл