Элементы сетевого планирования и управления (Варианты заданий к расчетно-графическим работам), страница 19

7 Задача выбора технических решений в условиях неопределённости и риска

Теоретические сведения. Принятие решений в условиях неопределённости и риска.

Основная входная информация для подобного класса задач – матрица решений, и результаты анализа ситуации принятия решения. Матрица имеет вид:

Под результатом решения e_ij будем понимать оценку, соответствующую варианту решения E_i (i=1,2,…,m) и условию (внешнему состоянию) F_j (j=1,2,…,n) и характеризующую экономический эффект (прибыль, убыток), полезность или надежность изделия.

Критерии принятия решений в условиях неопределенности и риска. Анализ ситуации принятия решений

Минимаксный критерий (ММ-критерий). Этот критерий использует оценочную функцию, соответствующую позиции крайнего пессимизма:

                            Z_MM = e_ir, e_ir = e_ij,                             (5.8)

т. е. множество оптимальных решений E₀ определяется соотношением

E₀ = {E_i0 | E_i0 Î E ^ e_i0 = e_ij}.                 (5.9)

Выбранные таким образом варианты полностью исключают риск. Однако это достоинство стоит некоторых потерь. Применение ММ-критерия бывает оправдано, если ситуация характеризуется обстоятельствами:

– о возможности появления состояний F_j ничего не известно;

– решение реализуется один или очень малое число раз;

– необходимо исключить какой бы то ни было риск.

Критерий Севиджа (S-критерий). Оценочная функция критерия Севиджа имеет вид

                     Z_S = e_ir = {e_ij – e_ij}                   (5.10)

и множество оптимальных вариантов решения строится следующим образом:

E₀ = {E_i0 | E_i0 Î E ^ e_i0 = e_ir}.                 (5.11)

Для понимания величины a_ij = e_ij – e_ij нужно трактовать как дополнительный выигрыш, если вместо варианта E_i в состоянии F_j выбрать другой, оптимальный для этого внешнего состояния результат.

Условия для применения критерия Севиджа такие же как и для ММ-критерия.

Критерий Байеса-Лапласа (BL-критерий). Пусть q_j – вероятность появления внешнего состояния F_j, тогда для критерия Байеса-Лапласа оценочная функция примет вид

Z_BL = e_ir, e_ir = 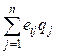,                         (5.12) т. е.           E₀ = {E_i0 |E_i0 Î E ^ e_i0 =  ^ }.

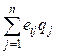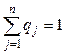Применение критерия рекомендуется, если ситуация характеризуется следующим образом:

– вероятности появления состояний F_j известны и не зависят от времени;

– решение реализуется (теоретически) бесконечно много раз;

– для малого числа реализаций решения допускается некоторый риск.

7 Задача выбора технических решений в условиях неопределённости и риска (вар 1-30)