Элементы сетевого планирования и управления (Варианты заданий к расчетно-графическим работам), страница 4

Варианты заданий № 31-40

Таблица – Продолжительность  выполнения работ

№ вар	Время
	1.2	1.3	1.5	2.4	2.5	3.5	3.6	3.9	4.7	4.8	5.7	5.8	5.9	5.10	6.9	6.10	7.11	8.11	9.11	10.11
31	4	6	2	6	3	6	4	4	6	5	8	2	4	4	6	5	8	2	3	4
32	4	7	4	2	4	2	5	4	7	2	8	5	5	4	7	2	8	5	2	5
33	2	4	6	3	5	2	6	6	4	6	3	6	4	4	6	5	8	2	3	4
34	7	5	5	4	6	4	6	8	3	4	4	6	5	4	7	2	8	5	2	5
35	7	6	4	4	7	4	6	4	2	5	4	7	4	4	6	5	8	2	3	4
36	4	7	5	2	4	6	3	5	8	6	6	4	5	4	7	2	8	5	2	5
37	6	4	6	7	5	5	7	6	4	6	4	6	6	6	4	6	3	6	5	7
38	4	6	4	6	6	6	4	7	4	7	4	6	4	2	5	7	6	4	7	5
39	4	7	4	6	4	2	2	4	2	4	6	3	5	8	6	5	7	6	8	6
40	2	4	6	3	5	8	7	5	7	5	5	7	6	7	4	4	5	4	3	2

 № 3 Задача минимизации издержек производства с применением графического способа и метода множителей Лагранжа

Требуется:  1) Постановка задачи;  2) Составить математическую модель; 3) Решить задачу графическим методом;

4) Решить задачу методом множителей Лагранжа; 5) Вывод.

1. Постановка задачи. По плану производства продукции предприятию необходимо изготовить N изделий. Эти изделия могут быть изготовлены двумя технологическими способами. При производстве x₁ изделий первым способом затраты равны  (денежных единиц), а при изготовлении x₂ изделий вторым способом они составляют  (д. е.). Определить, сколько изделий каждым из способов следует изготовить, так чтобы общие затраты на производство продукции были минимальными.

Решение. 2. Математическая постановка задачи состоит в определении минимального значения функции

При условии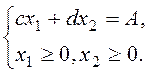   

Задача минимизации издержек производства с применением графического способа и метода множителей Лагранжа

№	варианта	№		№
1		11		21
2		12		22
3		13		23
4		14		24
5		15		25
6		16		26
7		17		27
8		18		28
9		19		29
10		20		30