Применение математической статистики при обработке результатов анализа

ПРИМЕНЕНИЕ   МАТЕМАТИЧЕСКОЙ   СТАТИСТИКИ

ПРИ   ОБРАБОТКЕ   РЕЗУЛЬТАТОВ АНАЛИЗА

Ошибки измерений. Во всякой экспериментальной работе большое значение имеет точность измерений, воспроизводимость и правильность результатов анализа. Опыт показывает, что любая измеряемая величина имеет свою ошибку; это обусловлено несовершенством приборов, их ограниченной точностью, влиянием внешних условий, потерей вещества, загрязнениями, неправильно проведенными записями и пр.

Кроме того, при измерениях могут появляться ошибки от ряда причин, природа которых остается неизвестной. Поэтому в результате эксперимента аналитик всегда устанавливает только приближенное значение определяемой величины, но никогда не может получить истинного ее значения . Вследствие этого измеряемая величина имеет некоторую ошибку, величину которой принято определять как абсолютную и относительную ошибку.

Абсолютной ошибкой М измеряемой величины называют разницу между полученным результатом измерения X и истинным (или более достоверным) значением А определяемой величины:

М = А - X,(97)

Абсолютную ошибку определяют в абсолютных единицах, ее размерность отвечает размерности измеряемой величины.

Относительной ошибкой V измеряемой величины называют отношение абсолютной ошибки М к точному значению А определяемой величины:

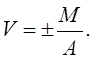                                                 (1)

Но так как истинное значение измеряемой величины неизвестно и абсолютная ошибка М очень мала по сравнению с величинами Л и X, то в формуле (1) величину А можно заменить очень близкой к ней величиной X. Тогда относительная ошибка будет определяться по формуле

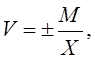                                                       (2)

откуда

                                             (3)

Относительная ошибка, как видно из формулы (2), является отношением двух величин одной и той же размерности, поэтому относительные ошибки — всегда безразмерные величины. Относительную ошибку, как правило, выражают в процентах

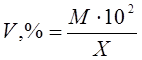                                                 (4)

В связи с этим возникает необходимость оценить степень приближения определяемой величины к истинному ее значению, иными словами, дать оценку точности полученных данных эксперимента, а в некоторых случаях выяснить и устранить причины, обусловливающие появление ошибок.

Цель будет достигнута, если для обработки экспериментальных данных применить методы математической статистики, сформулированные в теории ошибок.

Все ошибки разделяют на систематические, случайные и грубые (промахи).

Систематические сшибки зависят от неправильных показаний измерительных приборов, неправильно градуированных приборов, мерных колб, пипеток, бюреток, невыверенных разновесов и др. Систематические ошибки должны быть устранены. Для этого перед работой все приборы необходимо прокалибровать, неисправные заменить на исправные и т. д. В показания выверенных приборов следует внести соответствующие поправки.

Случайные ошибки возникают от различных помех, несовершенства органов чувств экспериментатора и других случайных причин. Ограниченная точность приборов, изменение условий, при которых проводится опыт (особенно это имеет значение при параллельных определениях), также приводят к возникновению случайных ошибок. Устранить их при измерениях невозможно, однако, пользуясь методом теории ошибок, можно уменьшить их влияние на результаты анализа и более точно установить вероятную ошибку в этих результатах.

Грубые ошибки в основном связаны с субъективными свойствами экспериментатора: невнимательностью и неряшливостью, занятием посторонними делами во время работы и др. Это приводит к неверным отсчетам, неправильным записям. При обработке результатов анализа грубые ошибки во внимание не принимают — их отбрасывают.

Метод математической статистики, применяемый для обработки результатов измерений, вполне оправдал себя в ряде областей науки. Однако в области химического анализа его применение еще недостаточно, хотя в этом имеется необходимость.

Известно, что анализ вещества сопровождается рядом массовых однотипных операций; это: взятие навески, растворение, градуировка мерной посуды, титрование, измерение силы тока и др. Все эти операции выполняются различными приборами, среди которых можно выделить совокупность таких однотипных приборов, как гальванометры, аналитические весы, микропипетки и многие другие. Поэтому работа аналитика относится к таким процессам, к которым можно применять методы математической статистики для обработки результатов эксперимента.

Широкое использование методов математической статистики для обработки экспериментальных данных, а также для оценки аналитических данных в любой лаборатории приносит очень большую пользу.

Нормальное распределение. Результаты каждого анализа представляют собой сумму большого числа взаимно независимых слагаемых (процессов взвешивания, растворения, осаждения и др.), которые подвергаются воздействию многообразных факторов. Поэтому можно считать, что случайные ошибки при всех химических анализах подчиняются закону нормального (гауссовского) распределения вероятностей  и описываются уравнением: