Закон нормального распределения вероятностей применим для большого числа (п) измерении или наблюдений так называемой генеральной совокупности явлений. Установлено, что нормальное распределение применимо для наблюдений при п > 20. В связи с этим классическая теория ошибок, основанная на нормальном распределении, неприменима для обработки малого числа измерений.
С начала XX в. в математической статистике стало разрабатываться новое направление, которое получило название статистики малых выборок, или микро-статистики. Очень большое практическое значение для малых выборок получило открытое в 1908 г. английским химиком и статистиком Гассетом t-распределение, получившее название распределения Стьюдента (Стьюдент — псевдоним Гассета).
Распределение Стьюдента зависит от числа степеней свободы, по которым определяется среднее квадратическое отклонение, т. е. выборочная дисперсия. Число степеней свободы обозначают буквой k и рассчитывают по формуле k = п — 1. Соотношение между кривыми нормального распределения и кривыми t-распределения для числа степеней свободы k = п — 1 = 1 и k = п — 1 = 5 показано на рис. 5. Как видно из рисунка, кривые t-распределения по форме напоминают кривые нормального распределения, но при малых значениях числа степеней свободы k = п — 1 они очень медленно сближаются с осью абсцисс.
Как показали Комарь и др., для оценки экспериментального материала, полученного в аналитических лабораториях (где экспериментатор в силу специфики работы делает сравнительно ограниченное число измерений), можно применять методы статистической обработки экспериментальных данных, основанных на t-распределении для малых выборок.
В статистическом анализе при обработке экспериментального материала проводят четкое разграничение между параметрами малых выборок и параметрами генеральной совокупности. Греческими буквами обозначают все параметры генеральной совокупности, а латинскими — параметры милых выборок.
Для обработки результатов химического анализа с целью оценки точности метода и качества выполняемых аналитических работ (воспроизведение, правильность) с успехом можно применять метод математической статистики, разработанный для малого числа наблюдений. При этом полученную систему наблюдений рассматривают как случайную выборку из некоторой гипотетической генеральной совокупности явлений.
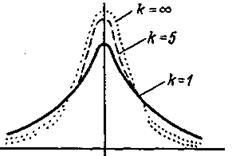
Рис. 5. Соотношение между нормальным распределением k = ¥ и t-распределением для k = 1 и k =5.
Оценка точности измерений. Результаты химических анализов являются приближенными числами. Нахождение наиболее вероятного их значения — одна из важнейших задач при обработке результатов анализа [2, 5—13].
Под вероятностью какого-либо явления принято понимать отношение числа случаев, благоприятствующих этому явлению, к числу всех случаев, образующих рассматриваемую группу. При этом считается, что вероятность появления всех случаев одинакова, поэтому нет оснований полагать, что какой-нибудь из случаев имеет больше, а другой меньше шансов осуществиться.
Например, в коробке находится 15 шаров, из них 8 белых, 4 синих и 3 желтых. Вероятность вынуть из коробки шар того или другого цвета будет соответственно равна: для белого — 8/15, для синего — 4/15 и для желтого — 3/15. Но из этой коробки нельзя вынуть черный шар, ибо его здесь нет; поэтому вероятность такого случая равна нулю. Если в коробке будут все шары синего цвета, то вероятность вынуть шар синего цвета равна единице.
Сумма вероятностей всех событий в рассматриваемой группе равна единице, иногда вероятности отдельно или их сумму выражают в процентах.
На основании закона нормального распределения случайных
ошибок показано, что арифметическое среднее ![]() из
результатов всех измерений является наиболее вероятным значением измеряемой
величины и определяется по формуле:
из
результатов всех измерений является наиболее вероятным значением измеряемой
величины и определяется по формуле:
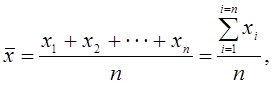
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.