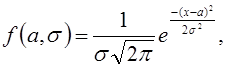(5)
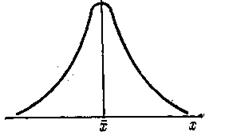
Рис. 1. Кривая нормального распределения.
где а — истинное значение определяемой величины; х — значение, полученное при данном измерении; s2 — дисперсия; s — среднее квадратическое отклонение; p и е — известные математические константы: p = 3,1416..., е — основание натуральных логарифмов (е = =2,1783).
Данная формула включает истинное значение определяемой величины а и выведена на основе предположения, что число измерений велико.
Кривая нормального распределения (рис. 1) симметрично распределяется относительно ординаты, проходящей через точку х-х на оси абсцисс, и асимптотически приближается к оси абсцисс.
В практике обычно пользуются нормированным распределением для удобства сравнения различных распределений, данные которых выражают в единой форме. При этом частоты или вероятности выражают в относительных числах, в долях единицы или процентах, приняв полную вероятность за единицу или за 100%, а значения варьирующего признака — не в именованных единицах, а в так называемых нормированных отклонениях, долях среднего квадратического отклонения s, которые обозначаются буквой t.
Нормированные отклонения определяются по формуле:
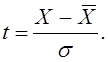
Нормирование сводится к тому, что начало координат переносят в центр распределения х, а по оси абсцисс откладывают отклонения х от х, выраженное в долях s, т. е.
.
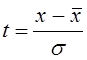На оси ординат откладывают частоты в долях единицы или процентах.
При таком способе получения кривых нормального
распределения, несмотря на большие различия их по форме, площадь, образуемая
ими с осью абсцисс, будет для них всегда равна единице при любых значениях 
и s .
Отсюда следует, что форма кривой нормального распределения зависит от среднего квадратического отклонения s. Если значения среднего квадратического отклонения малы, то кривая имеет иглообразную форму, а если они больше, кривая становится пологой.
На рис. 173 приведены три кривые нормального
распределения результатов измерения с равными х и различными значениями
s, т. е. s1 = 1; s2 = 2; s3 = 4, подтверждающие это. Наблюдаемые отклонения
варьирующего признака от х влево и вправо определяются величиной s и
в основном укладываются в границах трех квадратических отклонений ±3s
или трех нормированных отклонений ±3t, потому что t выражено в s. Из рис. 174 видно, что в
пределах 
укладывается основная масса всех наблюдений
(68,3%, т. е. около 2/з). Поэтому s называется основным
отклонением. В пределах 
находится 95,5%, а в
пределах 
— 99,7% всех наблюдений, т. е. укладываются
почти все наблюдаемые отклонения вариационного ряда. Продолжение кривой за
пределы практического значения не имеет, так как
вероятность встретить значение варьирующего признака, превышающего на 
, равна только
0,3%, т. е. 3 наблюдения на 1000 могут отклоняться больше чем на .
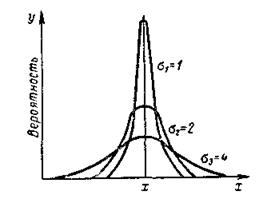
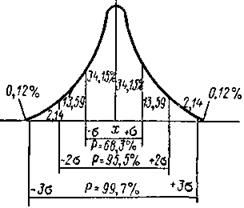
Рис. 2. Кривая нормального
рас- Рис. 3. Теоретические полигоны пределенияс различными значения- вариаций,
включающие число слуми сигмы. чаев в пределах: 
В практической работе считают возможным пользоваться вероятностями, которые соответствуют величинам ±2s (±2t) и ±3s (±3 t). Вероятность для: ±2s (±2 t) выражают округленной величиной 0,95, или 95%, а для: ±3s (±3t) — 0,99, или 99%. Эти вероятности называют доверительными вероятностями или надежностями, и обозначают a; это значения, которыми можно уверенно пользоваться.
В работе при использовании вероятности 0,95 (95%) риск сделать ошибку составляет 0,05 (5%), или 1 раз на 20, а при вероятности 0,99 (99%) возможность ошибиться составляет 0,01 (1%), или 1 раз на 100. Величины 0,05 (5%) и 0,01 (1%) получили название уровней значимости.
Выбор в работе доверительной вероятности, т. е. надежности, или уровня значимости для тех или иных исследований подсказывается практическими соображениями и возможностями, а также ответственностью выводов. В аналитической работе обычно принимают двусигмовые пределы за допустимые отклонения, а величину ±2s называют максимальной допустимой ошибкой. Рекомендуется пользоваться доверительной вероятностью, т. е. надежностью a= 0,95.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.