Применение математической статистики при обработке результатов анализа, страница 4

где x₁, x₂, … , х_п — результаты отдельных измерений; п — число параллельных измерений;  — среднее арифметическое значение определяемой величины, оно Принимается за приближенное значение истинного числа и записывается

В случаях, когда для оценки пользуются средними арифметическими данными, имеющими различную достоверность, одним данным придают большее значение, другим — меньшее. Например, получены данные результатов анализа 0,25% и 0,31%; допустим, что первому результату придается большее значение, т. е. больший нес, например 2, а второму меньший — 1. Тогда среднее арифметическое вычисляют так:

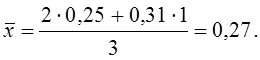
Но этим приемом определения среднего арифметического следует пользоваться с чрезвычайно большой осторожностью, так как он может внести заметную субъективную ошибку.

Отклонение случайной измеряемой величины от среднего арифметического принято в теории ошибок называть дисперсией или рассеиванием.

Дисперсия в достаточной степени характеризует воспроизводимость метода. Установлено, что чем меньше точность измерений, тем больше дисперсия, и наоборот — при более точных измерениях дисперсия мала.

Дисперсия в малых выборках обозначается символом S² и вычисляется по формуле:

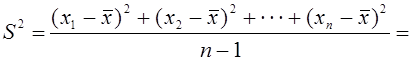
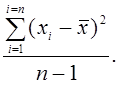 (6)

Корень квадратный из величины выборочной дисперсии называется стандартным отклонением или средним квадратическим отклонением (S) отдельного определения от средней арифметической. Оно вычисляется по формуле:

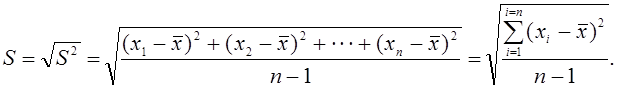 (7)

При  оценке точности полученных  результатов анализа вычисляют выборочную дисперсию средней квадратической S-. Для этого пользуются формулой

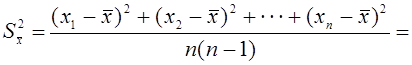
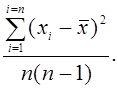 (8)

Квадратный корень из этой величины называется средней квадратической ошибкой  среднего  арифметического  и   вычисляется   по  формуле:

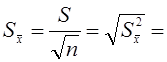
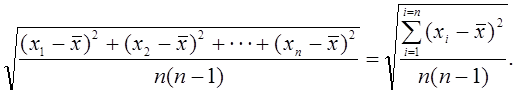  (9)

Точность прямого измерения характеризуется величиной , которая равна абсолютной величине разности между средней арифметической к и истинным значением измеряемой величины а. Его рассчитывают по формуле:

 (10)

или

 (11)

где a — доверительная вероятность, или надежность (в практической работе больше всего пользуются надежностью 0,95, реже — 0,99 и еще реже — надежностью 0,999); t_a,_k — коэффициент нормированных отклонений при малой выборке, который зависит от п и a. Числовые значения t_a,_k  для различных a и k = п — 1 приведены в табл. 1, где п — число измерений, a k — число степеней свободы.

Таблица 1

Значения t_a,_k  для различных а и k