Для характеристики точности метода кроме ![]() рассчитывают его вероятную относительную
ошибку по формуле
рассчитывают его вероятную относительную
ошибку по формуле
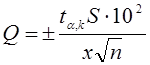 (12)
(12)
или
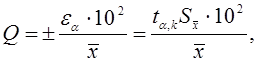 (13)
(13)
где ta,k —
множитель, зависящий от надежности и от числа степеней свободы k = п — 1; ![]() — средняя
арифметическая из п числа определений.
— средняя
арифметическая из п числа определений.
Для характеристики относительной пестроты или выравненности варьирующего признака в изучаемом явлении определяют коэффициент вариаций или изменчивости.
Коэффициентом вариации (изменчивости) называют отношение среднего квадратического отклонения, выраженного в процентах, к среднему арифметическому. Его обозначают V и вычисляют по формуле
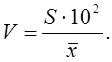 (14)
(14)
Чем больше V, тем относительно больше пестрота и меньше выравненность изучаемых явлений, и наоборот.
Коэффициент вариации, будучи отвлеченным числом, выраженным в процентах, дает возможность сравнивать варьирование признаков разной размерности.
Ё При небольшом числе измерений кроме определения точности прямого измерения, т. е. ea, вычисляют еще доверительный интервал (предел), или интервальное значение измеряемой величины. Интервальным значением или доверительным пределом называют границы, в пределах которых с_надежностью a находится__истинное__значение измеряемой величины а.
Доверительный предел измеряемой величины рассчитывают по формуле
![]() (14)
(14)
и
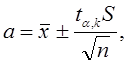 (15)
(15)
или
![]() (16)
(16)
В теории ошибок установлено, что, пользуясь
этими уравнениями, можно достаточно точно оценить приближенное равенство ![]() .
.
При малом числе измерений, кроме доверительного предела (или так называемого интервального значения) измеряемой величины требуется вычислить и приближенно оценить значение стандартного отклонения s для генеральной совокупности. При этом допускают, что стандартное отклонение для генеральной совокупности s приближенно равно средней квадратической ошибке отдельного определения S при малом числе измерений, т. е. s » S.
В этом случае интервальное значение s будет вычисляться так:
![]() (17)
(17)
где ![]() —
точность стандартного отклонения, найденная при надежности a и
числе степеней свободы k = п — 1 по формуле
—
точность стандартного отклонения, найденная при надежности a и
числе степеней свободы k = п — 1 по формуле ![]()
![]() — множитель, который зависит от надежности
a и числа степеней свободы k = п — 1 (табл. 2); S — среднее
квадратическое отклонение отдельного определения. При вычислении и оценке
границ s допускают, что для q > 1 левая доверительная граница интервального значения s равна нулю. Тогда формула для расчета и оценки стандартного
отклонения будет иметь вид:
— множитель, который зависит от надежности
a и числа степеней свободы k = п — 1 (табл. 2); S — среднее
квадратическое отклонение отдельного определения. При вычислении и оценке
границ s допускают, что для q > 1 левая доверительная граница интервального значения s равна нулю. Тогда формула для расчета и оценки стандартного
отклонения будет иметь вид:
0<s <S+da. (18)
Если истинное число а известно и обработка экспериментальных данных показывает, что
![]() (19)
(19)
значит, в измерениях допущена систематическая ошибка Е . Доверительный предел ее может быть найден по формуле:
![]() (20)
(20)
Следовательно, полученные после
статистической обработки экспериментальных данных значения 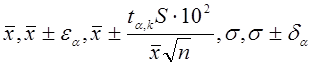 позволяют полностью определить
точность, правильность и воспроизводимость проводимых наблюдений.
позволяют полностью определить
точность, правильность и воспроизводимость проводимых наблюдений.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.