Физика \ Медицинская и биологическая физика с основами высшей математики

Применение математической статистики при обработке результатов анализа, страница 7

Можно применить и другой способ обнаружения расхождений между результатами анализа. Для этого используют отношение дисперсий S2, причем при расчете в числитель ставят всегда большую дисперсию, а в знаменатель — меньшую:

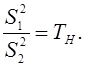                                                (23)

Дисперсию   S2  вычисляют  по   формуле   (8).

Отношение ТH будет тем больше, чем больше расхождения между сравниваемыми дисперсиями. Известно, что обе дисперсии будут уменьшаться и приближаться к одной и той же величине, если число измерений nl и п2 будет увеличиваться; при этом отношение дисперсий будет стремиться к единице.

При малом числе измерений отношение ТH будет отклоняться от единицы за счет случайных воздействий, тем больше, чем меньше kl и k2 (а следовательно, и чем меньше п1 и п2).

Вычисленное отношение дисперсий ТH сравнивают с отношением Тa, найденным с надежностью a = 0,95 по табл. 3.

Таблица 3

Значения ТH для доверительной вероятности P = 0,05

Зна-

чения k,

3начения     k1

1

2

3

4

5

6

8

12

24

¥

1

164,45

199,50

215,72

224,57

230,17

233,97

338,89

243,91

249,04

254,32

2

18,51

19,00

19,16

19,25

19,30

19,33

19,37

19,41

19,45

19,50

3

10,13

9,55

9,28

9,12

9,01

8,94

8,84

8,74

8,64

8,53

4

7,71

6,94

6,59

6,39

6,26

6,16

6,04

5,91

5,77

5,63

5

6,61

5,79

5,41

5,19

5,05

4,95

4,82

4,68

4,53

4,38

6

5,99

5,14

4,76

4,53

4,39

4,28

4,15

4,00

3,84

3,67

7

5,59

4,74

4,35

4,12

3,97

3,87

3,73'

3,57

3,41

3,23

8

5,32

4,46

4,07

3,84

3,69

3,58

3,44

3,28

3,12

2,93

9

5,12

4,26

3,88

3,63

3,48

3,37

3,23

3,07

2,90

2,71

10

4,96

4,10

3,71

3,48

3,33

3,22

3,07

2,91

2,74

2,54

И

4,84

3,98

3,59

3,36

3,20

3,09

2,95

2,79

2,61

2,40

12

4,75

3,88

3,49

3,26

3,11

3,00

2,85

2,69

2,50

2,30

13

4,67

3,80

3,41

3,18

3,02

2,92

2,77

2,60

2,42

2,21

14

4,60

3,74

3,34

3,11

2,96

2,85

2,70

2,53

2,35

2,13

15

4,54

3,68

3,29

3,06

2,90

2,79

2,64

2,48

2,29

2,07

16

4,49

3,63

3,24

3,01

2,85

2,74

2,59

2,42

2,24

2,01

17

4,45

3,59

3,20

2,98

2,81

2,70

2,55

2,38

2,19

,98

18

4,41

3,55

3,16

2,93

2,77

2,68

2,51

2,34

2,15

,92

19

4,38

3,52

3,13

2,90

2,74

2,63

2,48

2,31

2,11

,88

20

4,35

3,49

3,10

2,87

2,71

2,60

2,45

2,28

2,08

,84

21

4,32

3,47

3,07

2,84

2,68

2,57

2,42

2,25

2,05

,81

22

4,30

3,44

3,05

2,82

2,68

2,55

2,40

2,23

2,03

,78

23

4,28

3,42

3,03

2,80

2,64

2,53

2,38

2,20

2,00

,76

24

4,26

3,40

3,01

2,78

2,62

2,51

2,36

2,18

1,98'

,73

25

4,24

3,38

2,99

2,76

2,60

2,49

2,34

2,18

1,98

,71

26

4,22

3,37

2,98

2,74

2,59

2,47

2,32

2,15

1,95

,69

27

4,21

3,35

2,96

2,73

2,57

2,46

2,30

2,13

1,93

,67

28

4,20

3,34

2,95

2,71

2,56

2,44

2,29

2,12

1,91

,65

29

4,28

3,33

2,95

2,70

2,56

2,43

2,28

2,10

1,90

,64

30

4,17

3,32

2,92

2,69

2,53

2,42

2,27

2,09

1,89

,62

35

4,12

3,26

2,87

2,64

2,48

2,37

2,22

2,04

1,83

1,57

Скачать файл