Физика \ Медицинская и биологическая физика с основами высшей математики

Применение математической статистики при обработке результатов анализа, страница 6

k	a			k	a
k	0,95	0,99	0,999	k	0,95	0,99	0,999
1	2	3	4	1	2	3	4
1	14,947	77,786	397,947	50	0,209	0,297	0,424
2	3,415	9,978	30,802	60	0,186	0,268	0,375
3	1,914	4,111	10,112	70	0,172	0,242	0,339
4	1,372	2,670	5,637	80	0,160	0,224	0,311
5	1,091	2,006	3,877	90	0,150	0,209	0,289
6	0,915	1,624	2,977	100	0,142	0,196	0,271
7	0,797	1,377	2,424	150	0,115	0,159	0,220
8	0,711	1,203	2,055	200	0,099	0,135	0,184
9	0,645	1,076	1,796	250	0,089	0,120	0,162
10	0,593	0,977	1,599	300	0,081	0,109	0,146
12	0,515	0,833	1,327	400	0,075	0,100	0,134
14	0,460	0,733	1,145	450	0,070	0,093	0,124
16	0,418	0,659	1,013	500	0,066	0,088	0,116
18	0,385	0,602	0,916	600	0,057	0,076	0,099
20	0,358	0,556	0,838	700	0,053	0,070	0,091
25	0,310	0,473	0,700	800	0,049	0,065	0,085
30	0,276	0,416	0,609	900	0,048	0,061	0,080
35	0,253	0,375	0,544	1000	0,044	0,058	0,076
40	0,234	0,343	0,494	5000	0,020	0,028	0,037
45	0,219	0,318	0,455	10000	0,014	0,018	0,023

Часто в лабораторной работе анализ одного и того же образца бывает выполнен в одной лаборатории разными аналитиками, разными методами или просто в разное время в двух лабораториях, и получено два разных ответа.

Пусть в первой серии измерений сделано n_l анализов со средним их значением .Во второй серии опытов сделано п_г анализов со средним значением их . Необходимо выяснить, являются ли расхождения между результатами анализа и следствием случайных ошибок, связанных с точностью метода, или они вызваны более существенными недостатками.

Для получения ответа поступают следующим образом. Вычисляют средние квадратические ошибки по формуле (105) для анализов первой и второй серий. Для первой серии анализов среднюю квадратическую ошибку обозначают S₁, для второй S₂. Далее по формуле (21) рассчитывают S₀:

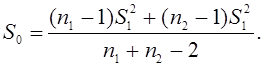(21)

Потом, пользуясь формулой

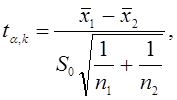(22)

подставляют в нее значения величин S₀, а также n₁ и п₂ и вычисляют величину t. В табл. 2 находят числовое значение t для надежности a = 0,95, принимая во внимание, что число степеней свободы будет вычисляться по формуле k = n₁ + n₂ –2. Если вычисленное значение t_a,_k окажется больше значения t_a,k, найденного по табл. 2, или равным ему, это значит, что расхождение между данными анализа вызвано не случайными ошибками, а более серьезными причинами: различиями в постановке опытов, ухудшением качества работы на определенных участках выполнения анализа и другими факторами.

1 2 3 4 5 6 7 8 9

Скачать файл