Задание для студентов на практическое занятие №3 по теме
«Обыкновенные дифференциальные уравнения»
Цель занятия: Научиться решать примеры и задачи по данной теме
Вопросы теории ( исходный уровень)
1.Понятие об обыкновенных дифференциальных уравнениях.
2.Примеры составления и решения дифференциальных уравнений для медико-биологических задач (размножение бактерий, накопление и выведение лекарственных веществ, радионуклидов и т.п.).
Содержание занятия:
1.ответить на вопросы по теме занятия
2.решить примеры
Задачи и примеры
Выяснить, являются ли решениями данных дифференциальных уравнений, указанные функции:
1)
![]()
2)
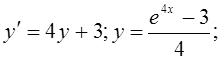
3)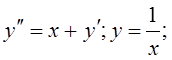
4)
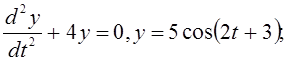
5)
![]()
6)
![]()
7)
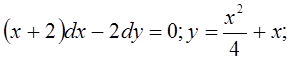
8)
![]()
9)
![]()
10)
![]()
Найти общее решение следующих дифференциальных уравнений:
1)
![]()
2)
![]()
3)
![]()
4)
![]()
5)
![]()
6)
![]()
7)
![]()
8)
![]()
9)
![]()
10)
![]()
11)
![]()
12)
![]()
13)
![]()
14)
![]()
15)
![]()
16)
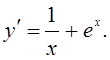
Найти частные решения дифференциальных уравнений:
1)
![]()
2)
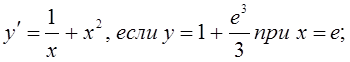
3)
![]()
4)
![]()
5)
![]()
6)
![]()
7)
![]()
Составив дифференциальные уравнения, решить задачи
1. Тело движется прямолинейно с ускорением а = 5 см/с2. Начальная скорость тела vo = 2 м/с. Вывести закон движения этого тела и вычислить путь, который оно пройдет за первые 10 мин движения.
2.Найти зависимость потенциальной энергии сжатой пружины от величины деформации.
Указание. Потенциальная энергия сжатой пружины равна работе силы F = Rx на пути от 0 до х.
3.Скорость охлаждения тела пропорциональна разности температур тела и окружающей среды. До какой температуры охладится тело за 30 мин, если за 10 мин оно охладилось от 100 до 60° С? Температура окружающей среды 20° С.
4.Уменьшение интенсивности света при прохождении через поглощающее вещество пропорционально интенсивности падающего света и толщине поглощающего слоя. Найти закон убывания интенсивности света, если известно, что при прохождении слоя l = 0,5 м интенсивность света убывает в два раза.
5.Найти закон убывания лекарственного препарата в организме человека, если через 1 ч после введения 10 мг препарата масса его уменьшилась вдвое. Какое количество препарата останется в организме через 2 ч?
6.Составить дифференциальное уравнение, описывающее движение математического маятника, считая, что углы отклонения маятника малы.
ОБЩИЕ ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ.
Понятие о дифференциальных уравнениях. Дифференциальные уравнения используются при изучении явлений и процессов в физике, химии, биологии, медицине, фармации, астрофизике, кибернетике, социологии и других областях знаний. Сформулировав задачу на языке дифференциальных уравнений, специалист любой отрасли знаний получает в руки готовый аппарат для численного решения задачи, изучения качественных особенностей этого решения. Многие вопросы естествознания и техники сводятся к нахождению неизвестной функции у = f(x), если известно уравнение, содержащее х, у и производные разных порядков функции f(x): f¢(x), f¢¢(x), …, f(n)(x) или дифференциалы функции df, d2f, …, dnf. Такие уравнения называются дифференциальными.
Рассмотрим задачу, приводящую к дифференциальному уравнению: установить закон изменения скорости u свободно падающего тела массой т без учета силы сопротивления воздуха.
Согласно второму закону Ньютона,
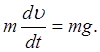
где mg – сила тяжести.
Полученное уравнение является дифференциальным, так как в него входит производная du/dt искомой функции u. Решить дифференциальное уравнение – значит найти такую функцию u = f(t) , которая тождественно удовлетворяет этому уравнению. Легко проверить, что уравнению удовлетворяет функция вида u = gt + C, где С – любое число. Указав начальные условия, можно найти одну функцию, удовлетворяющую уравнению. Так, если при t = 0 u = u0, то получим функцию u = u0 + gt.
Существует много задач из различных областей знаний, решение
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.