


























4. СОБСТВЕННЫЕ ВЕКТОРЫ И СОБСТВЕННЫЕ ЧИСЛА
ЛИНЕЙНОГО ПРЕОБРАЗОВАНИЯ
Определение. Если линейное отображение отображает пространство само в себя, то оно называется линейным преобразованием, т.е. здесь
![]()
![]() .
.
Все утверждения и теоремы
раздела 3 справедливы и для преобразований линейного пространства, но в общем
случае при определении матрицы линейного отображения ![]() выбирались
разные базисы в пространствах
выбирались
разные базисы в пространствах ![]() и
и ![]() . Если же
. Если же ![]() и
и ![]() совпадают, то логично пользоваться
одним и тем же базисом и для образов, и для прообразов, следовательно,
некоторые определения и формулы изменятся.
совпадают, то логично пользоваться
одним и тем же базисом и для образов, и для прообразов, следовательно,
некоторые определения и формулы изменятся.
Определение.
Матрицей линейного преобразования ![]() в
базисе
в
базисе ![]() называется матрица, столбцы которой есть
координаты векторов
называется матрица, столбцы которой есть
координаты векторов ![]() в базисе е(координаты
образов базисных векторов в том же базисе).
в базисе е(координаты
образов базисных векторов в том же базисе).
Матрица линейного преобразования квадратная порядка п.
В
соответствии с определением, при переходе от базиса е к базису е'матрица преобразования ![]() будет иметь вид
будет иметь вид
![]() (4.1)
(4.1)
(см. формулу (3.5)) ![]() , где теперь
, где теперь ![]() ).
).
Линейные преобразования обладают рядом специфических свойств, которые для отображений общего вида, вообще говоря, не справедливы. Это связано с тем, что образы и прообразы векторов лежат в одном пространстве, и мы получаем возможность говорить об их взаимном расположении.
Определение.
Ненулевой вектор ![]() называется собственнымвектором преобразования
называется собственнымвектором преобразования ![]() , если
, если ![]() , при этом число
, при этом число ![]() называется
собственным значением (собственным числом),
соответствующим собственному вектору
называется
собственным значением (собственным числом),
соответствующим собственному вектору ![]() .
.
Если в ![]() выбран
базис, то
выбран
базис, то
![]() .
.
Пусть Е – единичная матрица порядка п, тогда последнее равенство можно записать в виде
![]()
или
![]() .
(4.2)
.
(4.2)
В координатах это равенство выглядит так
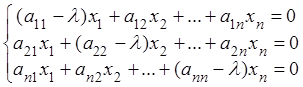
– однородная система линейных уравнений порядка n.
Если ![]() , то
система имеет единственное решение
, то
система имеет единственное решение
![]() , но собственным вектором мы назвали
ненулевой вектор, следовательно, для существования такого вектора необходимо
потребовать, чтобы
, но собственным вектором мы назвали
ненулевой вектор, следовательно, для существования такого вектора необходимо
потребовать, чтобы
![]() .
(4.3)
.
(4.3)
Это уравнение называется характеристическим уравнением.
Левая
часть равенства (4.3) – многочлен степени п, который называется
характеристическим многочленом преобразования ![]() :
:
![]()
Теорема
4.1. Если ![]() и
и ![]() –
матрицы преобразования
–
матрицы преобразования ![]() в разных базисах, то
характеристические многочлены этих матриц совпадают (собственные числа преобразования
в разных базисах, то
характеристические многочлены этих матриц совпадают (собственные числа преобразования
![]() в разных базисах одинаковы, т.е. не зависят
от выбора базиса!).
в разных базисах одинаковы, т.е. не зависят
от выбора базиса!).
Доказательство.
Если ![]() и
и ![]() - два базиса в
- два базиса в ![]() и
и ![]() матрица перехода от
матрица перехода от ![]() к
к ![]() , то по
формуле (4.1)
, то по
формуле (4.1)
![]() ,
,
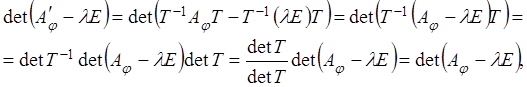
т.е.
характеристические многочлены матриц ![]() и
и ![]() совпадают, следовательно, собственные
числа одинаковы.
совпадают, следовательно, собственные
числа одинаковы.
Теорема
4.2. Если собственные векторы ![]() преобразования
преобразования ![]() соответствуют различным собственным
значениям, то они линейно независимы.
соответствуют различным собственным
значениям, то они линейно независимы.
Доказательство.
1) ![]() ,
, ![]() – два
собственных вектора, соответствующие собственным числам
– два
собственных вектора, соответствующие собственным числам ![]() ,
,
![]() ,
, ![]() .
.
Составим
линейную комбинацию этих векторов и приравняем её к ![]()
![]() .
(*)
.
(*)
Применим
преобразование ![]() к обеим частям этого равенства.
Получим
к обеим частям этого равенства.
Получим
![]() ,
, ![]() ,
, ![]() .
.
Умножим
(*) на ![]() :
: ![]() .
.
Вычитая
из одного равенства другое, получим ![]() , так как
, так как ![]() по условию, а
по условию, а ![]() по
определению, то
по
определению, то ![]() .
.
Подставляем
в (*) ![]() , получаем
, получаем ![]() , так
как по определению
, так
как по определению ![]() , следовательно
, следовательно ![]() , т.е. линейная комбинация должна быть
тривиальной, что равносильно тому, что векторы
, т.е. линейная комбинация должна быть
тривиальной, что равносильно тому, что векторы ![]() ,
, ![]() – линейно независимы.
– линейно независимы.
2)
Пусть утверждение справедливо для ![]() векторов, покажем, что
тогда оно справедливо и для
векторов, покажем, что
тогда оно справедливо и для ![]() векторов.
векторов.
Пусть
система векторов ![]() удовлетворяет условию теоремы.
Рассмотрим равную нулю линейную комбинацию этих векторов
удовлетворяет условию теоремы.
Рассмотрим равную нулю линейную комбинацию этих векторов
![]() .
(**)
.
(**)
Подействуем
преобразованием ![]() на это равенство, получим
на это равенство, получим
![]() .
.
Умножим
(**) на ![]() :
:
![]() .
.
Вычитая эти два равенства, находим
![]() , так как
, так как ![]() – линейно независимы, это значит, что в
левой части равенства записана тривиальная линейная комбинация, т.е.
– линейно независимы, это значит, что в
левой части равенства записана тривиальная линейная комбинация, т.е.
![]() , по условию теоремы
, по условию теоремы ![]() ,
, ![]() , …,
, …, ![]() , следовательно,
, следовательно,
![]() .
.
Подставим
![]() в (**), получим
в (**), получим ![]() ,
следовательно,
,
следовательно, ![]() , так как по определению
, так как по определению ![]() .
.
Таким
образом, ![]() – линейно независимы.
– линейно независимы.
Следствие
4.1. Если преобразование ![]() имеет п попарно
различных собственных значений, то существует базис из собственных векторов
этого преобразования!
имеет п попарно
различных собственных значений, то существует базис из собственных векторов
этого преобразования!
Теорема 4.3. Матрица линейного
преобразования ![]() в базисе е имеет
диагональный вид тогда и только тогда, когда все векторы базиса являются
собственными векторами преобразования
в базисе е имеет
диагональный вид тогда и только тогда, когда все векторы базиса являются
собственными векторами преобразования ![]() .
.
Другая
формулировка следствия 4.1. Если все корни характеристического многочлена
матрицы Аразличны, то существует невырожденная матрица Т(![]() ) такая, что матрица
) такая, что матрица ![]() – диагональная (Т – матрица перехода к базису из собственных
векторов).
– диагональная (Т – матрица перехода к базису из собственных
векторов).
5. ЕВКЛИДОВЫ ПРОСТРАНСТВА
5.1. Определение и основные свойства
Определение.
Линейное пространство ![]() называется евклидовым, если
в нем определена операция скалярного умножения, сопоставляющая любым двум
векторам
называется евклидовым, если
в нем определена операция скалярного умножения, сопоставляющая любым двум
векторам ![]() и
и ![]() число,
обозначаемое
число,
обозначаемое ![]() , и обладающая свойствами:
, и обладающая свойствами:
1) ![]() ;
;
2) ![]() ;
;
3) ![]() ;
;
4) ![]() ,
если
,
если ![]() ;
;
5)
![]() если
если ![]() .
.
Евклидово
пространство размерности побозначается ![]() .
.
Определение.
Длиной или модулем вектора называется число ![]() . Обозначается
. Обозначается ![]() , т.е. по определению
, т.е. по определению ![]() .
.
Определение. Углом
между векторами ![]() называется число, определяемое
из равенства
называется число, определяемое
из равенства
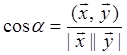
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.