Собственные векторы и собственные числа линейного преобразования. Билинейные и квадратичные формы, страница 4

6.1 Сопряженные и самосопряженные преобразования

Определение. Линейное преобразование  евклидова пространства  называется сопряженным данному линейному преобразованию , если  имеет место равенство

.                                              (6.1)

В более полных курсах доказывается, что любое преобразование имеет единственное сопряженное преобразование.

Предположим, что данное преобразование  имеет сопряженное . Выясним, как связаны их матрицы  и  в некотором базисе е. Используя равенство (5.2) перепишем (6.1) в матричной форме

где X, Y – координатные столбцы произвольных векторов  – матрица Грама базиса е, отсюда

  или  , так как  произвольные, следовательно, должно выполняться равенство

  или   , так как  – невырожденная матрица, у нее существует обратная и значит последнее равенство равносильно тому, что

                                                  (6.2)

Часто сопряженное преобразование обозначается через , т.е. , тогда матрицы этих преобразований обозначаются .

В частности, если базис е ортонормированный, то  и из (6.2)

                                                           (6.3)

Определение. Линейное преобразование  евклидова пространства  называется самосопряженным, если , т.е.

, или из (6.1)

Из формулы (6.3) получаем, что  преобразование является самосопряженным тогда и только тогда, когда его матрица симметрическая (в любом базисе удовлетворяет условию ).

В силу сказанного, часто самосопряженные преобразования называются симметрическими.

Теорема 6.1. Если  - самосопряженное преобразование евклидова пространства , то все его собственные числа действительные.

Доказательство. Рассмотрим частный случай . Найдём собственные числа, т.е. решим уравнение

.                                                     (*)

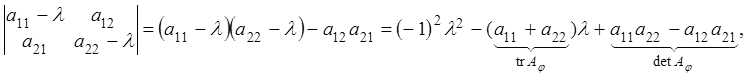
тогда (*) – квадратное  уравнение. Пусть  – дискриминант этого квадратного уравнения.

так как  – самосопряжённое преобразование ,  и , следовательно : , из чего заключаем, что корни характеристического многочлена действительные.

Теорема 6.2. Если  - самосопряженное преобразование евклидова пространства , то собственные векторы, соответствующие различным собственным значениям этого преобразования, ортогональны.

Доказательство. Пусть  – собственные числа самосопряжённого преобразование , , а  и  – соответствующие им собственные векторы, т.е. , , тогда

Вычитая одно равенство из другого, получаем

, где  по условию, следовательно, , что означает  .

Теорема 6.3. Если  - самосопряженное преобразование евклидова пространства , то в существует ортонормированный базис из собственных векторов преобразования .

Эта теорема допускает матричную формулировку.

Теорема 6.4. Если A – симметрическая матрица, то существует ортогональная матрица U такая, что  – диагональная матрица. Здесь U – матрица перехода к ортонормированному базису из собственных векторов.

6.2. Ортогональные преобразования

Второй вид преобразований, которые следует рассмотреть – это ортогональные преобразования.

Определение. Преобразование  евклидова пространства  называется ортогональным, если оно сохраняет скалярное произведение, т.е.

.                                 (6.4)

Условие (6.4) очень сильное. Из него, в частности, следует, что  – линейное преобразование.

Действительно, рассмотрим произвольный вектор  и произвольное число , тогда используя свойства скалярного произведения получаем:

следовательно,    и свойство 1) в определении линейного преобразования установлено.

Аналогично, :

т.е.  и свойство 2) в определении линейного преобразования также установлено, т.е. любое ортогональное преобразование  – линейное!               

Теорема 6.5. В Евклидовом пространстве  в ортонормированном базисе ортогональное преобразование имеет ортогональную матрицу, т.е.

  .

Доказательство.  По формуле вычисления скалярного произведения в ортонормированном базисе , из формулы (6.4) получаем :