Собственные векторы и собственные числа линейного преобразования. Билинейные и квадратичные формы, страница 6

где Т матрица перехода от базиса е к базису f .

Доказательство. Так как Т – матрица перехода от е к  f, то , , где  – координатные столбцы вектора  в базисах е и  f соответственно, , то по формуле (7.2) получаем :

;

с другой стороны , следовательно, , так как  – произвольные, то выражение, стоящее в скобках должно быть равно нулю

 .

Следствие. Ранг матрицы  равен рангу матрицы . Это сразу вытекает из равенства (7.3) и из того, что ранг матрицы не изменяется при умножении на невырожденную матрицу.

Это позволяет ввести понятие ранга билинейной формы.

Определение. Рангом билинейной формы называется ранг матрицы этой формы в произвольном базисе.

Определение. Билинейная форма , заданная в , называется невырожденной (вырожденной), если ее ранг равен (меньше) размерности пространства, т.е.

             форма невырожденная;

             форма вырожденная.

7.2. Квадратичные формы

Пусть  - симметричная билинейная форма, заданная на линейном пространстве .

Определение. Квадратичной формой называется числовая функция  одного аргумента , значения которой совпадают со значениями билинейной формы  при .

При этом симметричная билинейная форма  называется полярной к квадратичной форме .

Пусть в  задана симметричная билинейная форма  в базисе . По формуле (7.1) , при этом в силу симметрии . Полагая в этом равенстве  получаем

                                                    (7.4)

представление квадратичной формы  в заданном базисе е.

Матрицу из коэффициентов  обозначим  и назовем матрицей квадратичной формы.

Матрица квадратичной формы при переходе к новому базису преобразуется по формуле (7.3), т.е.

                                                      (7.5)

где Т – матрица перехода к новому базису.

Так как матрица перехода всегда невырожденная, то ранг матрицы квадратичной формы не изменяется при переходе к новому базису.

Определение. Ранг матрицы квадратичной формы в произвольном базисе называется рангом квадратичной формы.

Если ранг квадратичной формы равен размерности пространства, то квадратичная форма называется невырожденной, в противном случае вырожденной.

Рассмотрим вопрос о приведении квадратичной формы к сумме квадратов, к так называемому каноническому виду, т.е. о выборе такого базиса  в , в котором квадратичная форма (7.4.) представляется в виде

                                    (7.6)

где  – координаты вектора  в базисе  f .

Коэффициенты  называются каноническими коэффициентами квадратичной формы, а базис  – каноническим базисом.

Метод Якоби

Пусть  – какой-либо базис в ,  – базис, в котором квадратичная форма  имеет канонический вид (канонический базис).

Рассмотрим преобразование вида

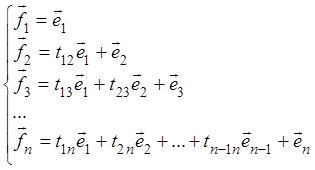     ,            (7.7)

которое называется треугольным, так как , где  верхняя треугольная матрица

.

Замечание. Так как определитель матрицы треугольного преобразования (7.7) отличен от нуля (), то векторы  образуют базис.

Введем в рассмотрение главные миноры матрицы  квадратичной формы  в базисе , обозначив их символами :

,   ,   ,   … ,

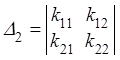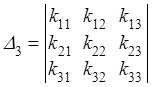,   где .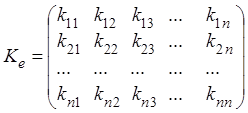

Теорема 7.4. Пусть :  , тогда существует единственное треугольное преобразование базиса , с помощью которого квадратичную форму  можно привести к каноническому виду.

Доказательство.  Коэффициенты квадратичной формы  в базисе  вычисляются по формуле , где  – полярная билинейная форма.

Если квадратичная форма  в базисе  имеет канонический вид то : , поэтому для доказательства теоремы достаточно с помощью треугольного преобразования базиса  построить базис , в котором  будут выполняться соотношения:

:   ,

(или, что тоже самое, при , так как  – симметричная).

Ввиду линейности билинейной формы  по каждому из аргументов, эти равенства будут выполняться, если будут выполнены равенства:

  (;  )                                   (*)

Действительно, используя линейность по первому аргументу, можем записать